题目内容
【题目】如图所示，半径为R的竖直光滑圆轨道与光滑水平面相切，质量均为m的小球A、B与轻杆连接，置于圆轨道上，A位于圆心O的正下方，B与O等高。它们由静止释放，最终在水平面上运动。下列说法正确的是
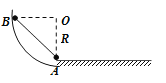
A. 下滑过程中重力对B做功的功率先增大后减小
B. 当B滑到圆轨道最低点时，轨道对B的支持力大小为3mg
C. 下滑过程中B的机械能增加
D. 整个过程中轻杆对A做的功为
【答案】AD
【解析】试题分析：根据重力和速度方向的关系判断重力功率的变化，AB小球组成的系统，在运动过程中，机械能守恒，根据机械能守恒定律求出到达最低点的速度，在最低点，根据牛顿第二定律求出轨道对B的支持力，下滑过程中，求出B重力势能的减小量和动能的增加量，从而判断机械能的变化量，整个过程中对A，根据动能定理求解轻杆对A做的功．
解：A、因为初位置速度为零，则重力的功率为0，最低点速度方向与重力的方向垂直，重力的功率为零，可知重力的功率先增大后减小．故A正确；
B、AB小球组成的系统，在运动过程中，机械能守恒，设B到达轨道最低点时速度为v，根据机械能守恒定律得：
，
解得：v=
在最低点，根据牛顿第二定律得：
N﹣mg=m
解得：N=2mg，故B错误；
C、下滑过程中，B的重力势能减小△EP=mgR，动能增加量
，所以机械能减小
，故C错误；
D、整个过程中对A，根据动能定理得：
，故D正确．
故选：AD
【题目】
实验小组要测量一节干电池的电动势和内电阻。实验室有如下器材可供选择：
A．待测干电池（电动势约为1.5V，内阻约为1.0
）
B．电压表（量程3V）
C．电压表（量程15V）
D．电流表（量程0.6A）
E．定值电阻（阻值为50
）
F．滑动变阻器（阻值范围0~50）
G．开关、导线若干
⑴为了尽量减小实验误差，在如图1所示的四个实验电路中应选用 。
⑵实验中电压表应选用 。（选填器材前的字母）
⑶实验中测出几组电流表和电压表的读数并记录在下表中。
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压U（V） | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
电流I（A） | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
请你将第5组数据描绘在图2中给出的U－I坐标系中并完成U－I 图线；
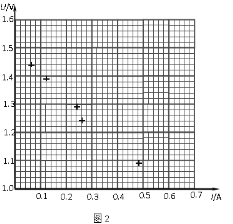
⑷由此可以得到，此干电池的电动势E=________V，内电阻r =________。（结果均保留两位有效数字）
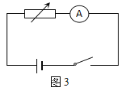
⑸有位同学从实验室找来了一个电阻箱，用如图3所示的电路测量池的电动势和内电阻。闭合开关后，改变电阻箱阻值。当电阻箱阻值为R1时，电流表示数为I1；当电阻箱阻值为R2时，电流表示数为I2。已知电流表的内阻为RA。请你用RA、R1、R2、I1、I2表示出电池的内电阻r = 。