题目内容
18．
如图所示，甲、乙、丙三个齿轮的半径分别为r1、r2、r3．若甲齿轮的角速度为ω1，则丙齿轮的角速度为（ ）| A． | $\frac{{r}_{1}{ω}_{1}}{{r}_{3}}$ | B． | $\frac{{r}_{3}{ω}_{1}}{{r}_{1}}$ | C． | $\frac{{r}_{3}{ω}_{1}}{{r}_{2}}$ | D． | $\frac{{r}_{1}{ω}_{1}}{{r}_{2}}$ |
分析 靠近齿轮接触，两轮边缘上各点线速度大小相等，根据v=rω计算从动轮的角速度．
解答 解：靠近齿轮接触，两轮边缘上各点线速度大小相等，可知甲、丙两轮边缘上各点线速度大小相等．
由v=rω得：ω1r1=ω3r3，则丙齿轮的角速度为ω3=$\frac{{r}_{1}{ω}_{1}}{{r}_{3}}$
故选：A．
点评 本题关键是明确同缘传动边缘点线速度相等，然后结合线速度与角速度关系公式v=rω列式分析．
练习册系列答案
相关题目
如图所示，一定质量的理想气体从状态A变化到状态B，再从状态B变化到状态C，已知状态A的温度为480K，求：
9．
如图，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝a、b、c和d，外筒的外半径为r．在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感应强度的大小为B．在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场．一质量为m、带电量为+q的粒子，从紧靠内筒且正对狭缝a的S点出发，初速为零．如果该粒子经过一段时间的运动之后恰好又回到出发点S，设两电极之间的电压大小为U，则（ ）
如图，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝a、b、c和d，外筒的外半径为r．在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感应强度的大小为B．在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场．一质量为m、带电量为+q的粒子，从紧靠内筒且正对狭缝a的S点出发，初速为零．如果该粒子经过一段时间的运动之后恰好又回到出发点S，设两电极之间的电压大小为U，则（ ）| A． | U=$\frac{{{B^2}q{r^2}}}{2m}$ | B． | U=$\frac{{{B^2}q{r^2}}}{m}$ | C． | U=$\frac{{{B^{\;}}qr}}{m}$ | D． | U=$\frac{{\sqrt{2}{B^2}q{r^2}}}{2m}$ |
13．伽利略对变速运动问题研究时，坚信自然界的规律是简洁明了的，他从这个信念出发，猜想落体一定是一种最简单的变速运动，而最简单的变速运动，它的速度应该是均匀变化的．但是，速度的变化怎样才算“均匀”呢？他考虑了两种可能：一种是速度的变化对时间来说是均匀的，即v与t成正比，另一种是速度的变化对位移来说是均匀的，即v与x成正比．后来发现，如果v与x成正比，将会推导出十分复杂的结论．那么，十分复杂的结论是什么呢？下面关于这个结论的说法正确的是（ ）
| A． | 物体运动的速度和时间之间的关系是二次函数关系 | |
| B． | 物体运动的位移和时间之间的关系是二次函数关系 | |
| C． | 物体所受的合外力与物体的速度成正比关系 | |
| D． | t=0时刻，初速度和位移均为零 |
3．
如图所示，质量分别为m1和m2的两个小球A、B，带有等量异种电荷，通过绝缘轻弹簧相连接，置于绝缘光滑的水平面上，突然加一个水平向右的匀强电场后，两小球A、B将由静止开始运动，在以后的运动过程中，对两小球A、B和弹簧组成的系统（设整个过程中不考虑电荷间库仑力的作用，且弹簧不超过弹性限度），以下说法正确的是（ ）
如图所示，质量分别为m1和m2的两个小球A、B，带有等量异种电荷，通过绝缘轻弹簧相连接，置于绝缘光滑的水平面上，突然加一个水平向右的匀强电场后，两小球A、B将由静止开始运动，在以后的运动过程中，对两小球A、B和弹簧组成的系统（设整个过程中不考虑电荷间库仑力的作用，且弹簧不超过弹性限度），以下说法正确的是（ ）| A． | 由于电场力对球A和球B做的总功为0，故小球电势能总和始终不变 | |
| B． | 由于两个小球所受电场力等大反向，故系统机械能守恒 | |
| C． | 当弹簧长度达到最大值时，系统机械能最小 | |
| D． | 当小球所受电场力与弹簧的弹力大小相等时，系统动能最大 |
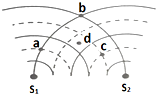如图所示，S1、S2是两个振幅相等的相干波源，实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷，其中d点处于图示波峰和波谷的正中间位置．在a、b、c、d四点中，振动加强点有bcd，振动减弱点有a，此时恰处于平衡位置的有ad．