��Ŀ����
����Ŀ����ͼ��ʾ���ڵ�һ���Ŀռ��д�����ǿ�糡����ǿ��y�Ḻ�����ڵ��������У�������ǿ�ų����ų�����ֱxyƽ�棨ֽ�棩���⣮һ����Ϊq������Ϊm�Ĵ�������˶����ӣ�����y����y=h���ĵ�P1ʱ����Ϊv0��������x��������Ȼ��x����x=2h����P2�����ų���������y����y=��2h����P3�㣬���ﵽx���ϵ�P4�㣨ͼ��δ����������������������
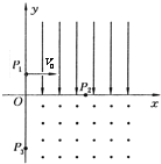
��1���糡ǿ�ȵĴ�С��
��2���Ÿ�Ӧǿ�ȵĴ�С��
��3����P1�˶���P4������ʱ��.
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�������������������1�������ڵ糡������ƽ���˶�����ţ�ٵڶ����ɼ��˶�ѧ��ʽ��������糡ǿ�ȣ���2����������������������������Բ���˶��İ뾶���ݼ��ι�ϵ�������������ţ�ٵڶ����ɼ�������Ÿ�Ӧǿ�ȣ���3���ֶ���ʱ�䣺�糡�������˶�ѧ��ʽ��ʱ�䣬�ų��������˶��˰�����ڣ�������ʱ�䣮
��1�������ڵڢ����ռ�����ƽ���˶���ˮƽ����![]() ����ֱ����
����ֱ����![]() �����
�����![]() ��
��
��2�����ӵ���![]() ��ʱ��
��ʱ��![]() ��
��![]() ��
��
�ٶȣ�![]() ��
��![]() ��
��![]() ���ٶ���x��н�
���ٶ���x��н�![]() ��
��
���ӹ켣��ͼ��ʾ��![]() ��
��![]() ����
����![]() ΪԲ��ֱ����
ΪԲ��ֱ����
Բ�ܰ뾶![]() ��
��
��ţ�ٵڶ����ɵã�![]() �����
�����![]() ��
��
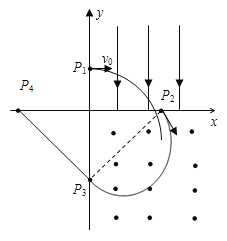
��3�����ӳ��ų�����![]() ������ֱ���˶����ɼ��ι�ϵ
������ֱ���˶����ɼ��ι�ϵ![]() ��
��
![]() ����
����![]() ��������-2h��0����
��������-2h��0����
�����ڵ糡�˶�ʱ�䣺![]() ��
��
�ڴų����˶�����Ϊ��![]() ��
��
�ڴų����˶�ʱ��Ϊ��![]() ��
��
������ֱ���˶�ʱ�䣺![]() ��
��
��P1��P4������ʱ�䣺![]() ��
��

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�