题目内容
14.宇航员站在一个星球表面,将一小球从离地面高为h处以初速度v0水平抛出,测出小球落地点与抛出点间的水平位移为x,若该行星的半径为R,万有引力常量为G.求该星球的质量M.分析 小球在星球表面做平抛运动,根据水平方向做匀速直线运动,竖直放置做自由落体运动求解重力加速度,再根据这个小球受的重力约等于行星给它的引力求解质量.
解答 解:对于小球平抛运动过程,有:$h=\frac{1}{2}{g_星}{t^2}$
x=v0t
解得:${g_星}=\frac{2hv_0^2}{x^2}$
由星球表面重力等于万有引力,则有$m{g_星}=G\frac{Mm}{R^2}$
解得:$M=\frac{{2hv_0^2{R^2}}}{{G{x^2}}}$
答:该星球的质量M为$\frac{2h{v}_{0}^{2}{R}^{2}}{G{x}^{2}}$.
点评 本题要抓住万有引力与平抛运动联系的桥梁是重力加速度g,知道根据万有引力等于重力是求星球质量的常用思路.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.质量为m的物体,在距地面h高处以$\frac{1}{3}$g的加速度由静止竖直下落到地面,下列说法中正确的是( )
| A. | 物体重力势能减少$\frac{1}{3}$mgh | B. | 物体的机械能减少$\frac{1}{3}$mgh | ||
| C. | 物体的动能增加mgh | D. | 重力做功mgh |
5.有一单摆,在海平面上某一段时间内摆动了N次,在该处某山顶上同样长的时间内摆动了N-1次,由此可知,此山的海拨高度是地球半径的( )
| A. | $\frac{1}{N-1}$倍 | B. | $\frac{1}{N}$倍 | C. | $\frac{1}{N+1}$倍 | D. | $\frac{N-1}{N+1}$倍 |
2.下列实验或器件应用涡流现象的是( )
| A. |  电磁感应实验 | B. |  日光灯电路 | C. |  直流电动机 | D. |  电磁灶 |
9.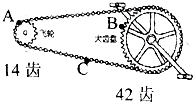 如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
 如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )| A. | A、B、C三点角速度大小相等 | |
| B. | A、B两点的线速度大小相等 | |
| C. | A、B两点的向心加速度之比为3:1 | |
| D. | 由图中信息,B、C两点的线速度之比为1:3 |
6.下列说法正确的是( )
| A. | 日心说的代表人物是哥白尼 | |
| B. | 太阳是静止不动的,地球和其他行星绕太阳转动 | |
| C. | 地球是绕太阳运动的一颗行星 | |
| D. | 日心说和地心说都是错误的 |
4.发现行星运动规律和万有引力定律的科学家分别是( )
| A. | 伽利略、开普勒 | B. | 开普勒、牛顿 | C. | 牛顿、卡文迪许 | D. | 伽利略、牛顿 |
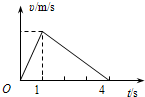 在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到最大时立即关闭发动机,继续向前滑行了一段时间后停止.运动过程的v-t图象如图.设汽车牵引力做功为W1,汽车在整个运动过程中克服阻力做功为W2,汽车的牵引力为F,汽车运动中受到的阻力为f,则:W1﹕W2=1:1;F﹕f=4:1.
在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到最大时立即关闭发动机,继续向前滑行了一段时间后停止.运动过程的v-t图象如图.设汽车牵引力做功为W1,汽车在整个运动过程中克服阻力做功为W2,汽车的牵引力为F,汽车运动中受到的阻力为f,则:W1﹕W2=1:1;F﹕f=4:1.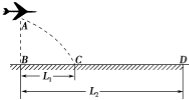 如图所示,在水平地面上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求:
如图所示,在水平地面上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求: