题目内容
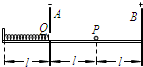 如图所示,A、B是两块竖直放置的平行金属板,相距为2l,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m、电荷量为q(q>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板l处有一固定档板,长为l的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小球,它将在电场力作用下由静止开始向左运动,穿过小孔(不与金属板A接触)后与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间T0第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开弹簧的瞬间,小球的电荷量都损失一部分,而变成刚与弹簧接触时小球电荷量的
如图所示,A、B是两块竖直放置的平行金属板,相距为2l,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m、电荷量为q(q>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板l处有一固定档板,长为l的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小球,它将在电场力作用下由静止开始向左运动,穿过小孔(不与金属板A接触)后与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间T0第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开弹簧的瞬间,小球的电荷量都损失一部分,而变成刚与弹簧接触时小球电荷量的| 1 | k |
(1)小球第一次接触薄板Q后,则弹簧的弹性势能多大;
(2)假设小球被第N次弹回两板间后向右运动的最远处恰好到达B板,小球从开始运动到被第N次弹回两板间向右运动到达B板的总时间.
分析:(1)小球在电场力作用下由静止开始向左运动,对于从小球开始释放到压缩弹簧到最短的过程,运用功能关系列式求解弹簧的弹性势能最大值.
(2)根据牛顿第二定律求出加速度,再根据运动学公式求解第一次接触Q时的速度大小.小球从第N次接触Q,到本次向右运动至最远处的时间包括两部分,一部分是小球从接触Q开始,经历时间T0第一次把弹簧压缩至最短,然后又被弹簧弹回,另一部分是离开Q向右做减速运动的过程.根据运动学公式进行求小球从第N次接触Q,到本次向右运动至最远处的时间TN的表达式,再求总时间.
(2)根据牛顿第二定律求出加速度,再根据运动学公式求解第一次接触Q时的速度大小.小球从第N次接触Q,到本次向右运动至最远处的时间包括两部分,一部分是小球从接触Q开始,经历时间T0第一次把弹簧压缩至最短,然后又被弹簧弹回,另一部分是离开Q向右做减速运动的过程.根据运动学公式进行求小球从第N次接触Q,到本次向右运动至最远处的时间TN的表达式,再求总时间.
解答:解:(1)对于从小球开始释放到压缩弹簧到最短的过程,根据功能关系得:
Ep=qEl.
(2)设小球第一次接触Q的速度为v,接触Q前的加速度为a.
根据牛顿第二定律有:qE=ma
对于小球从静止到与Q接触前的过程,根据运动学公式有v2=2al
联立解得:v=
小球每次离开Q的速度大小相同,等于小球第一次与Q接触时速度大小为:
v=
设小球第n次离开Q向右做减速运动的加速度为an,速度由v减为零
所需时间为tn,小球离开Q所带电荷量为qn,则有:
qnE=man
tn=
qn=
联立解得:tn=
kn
小球从第N次接触Q,到本次向右运动至最远处的时间为:
Tn=2T0+
kN,
故小球从开始运动到被第N次弹回两板间向右运动到达B板的总时间为:
T=T1+T2+…TN=2NT0+
(1+2k+2k2+2k3+…+2kN-1+kN)
答:(1)小球第一次接触薄板Q后,则弹簧的弹性势能为qEl;
(2)假设小球被第N次弹回两板间后向右运动的最远处恰好到达B板,小球从开始运动到被第N次弹回两板间向右运动到达B板的总时间为2NT0+
(1+2k+2k2+2k3+…+2kN-1+kN).
Ep=qEl.
(2)设小球第一次接触Q的速度为v,接触Q前的加速度为a.
根据牛顿第二定律有:qE=ma
对于小球从静止到与Q接触前的过程,根据运动学公式有v2=2al
联立解得:v=
|
小球每次离开Q的速度大小相同,等于小球第一次与Q接触时速度大小为:
v=
|
设小球第n次离开Q向右做减速运动的加速度为an,速度由v减为零
所需时间为tn,小球离开Q所带电荷量为qn,则有:
qnE=man
tn=
| v |
| an |
qn=
| q |
| kn |
联立解得:tn=
| mv |
| qE |
小球从第N次接触Q,到本次向右运动至最远处的时间为:
Tn=2T0+
|
故小球从开始运动到被第N次弹回两板间向右运动到达B板的总时间为:
T=T1+T2+…TN=2NT0+
|
答:(1)小球第一次接触薄板Q后,则弹簧的弹性势能为qEl;
(2)假设小球被第N次弹回两板间后向右运动的最远处恰好到达B板,小球从开始运动到被第N次弹回两板间向右运动到达B板的总时间为2NT0+
|
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.要注意小球运动过程中各个物理量的变化.

练习册系列答案
相关题目
 如图所示,a、b是两个带有同种电荷的小球,现用两根绝缘细线将它们悬挂于真空中同一点.已知两球静止时,它们离水平地面的高度相等,线与竖直方向的夹角分别为α、β,且α<β.现有以下判断,其中正确的是( )
如图所示,a、b是两个带有同种电荷的小球,现用两根绝缘细线将它们悬挂于真空中同一点.已知两球静止时,它们离水平地面的高度相等,线与竖直方向的夹角分别为α、β,且α<β.现有以下判断,其中正确的是( ) 电风扇的扇叶的重心如果不在转轴上,转动时会使风扇抖动,并加速转轴磨损.调整时,可在扇叶的一区域通过固定小金属块的办法改变其重心位置.如图所示,A、B是两调整重心的金属块(可视为质点),其质量相等,它们到转轴O的距离rA<rB.扇叶转动后,它们的( )
电风扇的扇叶的重心如果不在转轴上,转动时会使风扇抖动,并加速转轴磨损.调整时,可在扇叶的一区域通过固定小金属块的办法改变其重心位置.如图所示,A、B是两调整重心的金属块(可视为质点),其质量相等,它们到转轴O的距离rA<rB.扇叶转动后,它们的( )| A、向心力FA<FB | B、线速度大小相等 | C、向心加速度相等 | D、角速度大小相等 |
 如图所示,A、B是两块相同的均匀长方形砖块,质量为M,长度L,叠放在一起,且A相对于B的右端伸出
如图所示,A、B是两块相同的均匀长方形砖块,质量为M,长度L,叠放在一起,且A相对于B的右端伸出 (2011?锦州模拟)如图所示,A、B是两个位于固定斜面上的正方体物块,它们的质量相等,F是沿水平方向作用于A上的外力,已知A与B的接触面,A、B与斜面的接触面均光滑,下列说法正确的是( )
(2011?锦州模拟)如图所示,A、B是两个位于固定斜面上的正方体物块,它们的质量相等,F是沿水平方向作用于A上的外力,已知A与B的接触面,A、B与斜面的接触面均光滑,下列说法正确的是( ) 如图所示,A,B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键K闭合时,下列说法正确的是( )
如图所示,A,B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键K闭合时,下列说法正确的是( )