题目内容
17.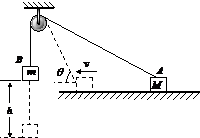 如图所示,跨过定滑轮的轻绳两端的物体A和B的质量分别为M和m,物体A在光滑水平面上,B由静止释放,当B沿竖直方向下降h时,这时细绳与水平面的夹角为θ,试求(空气阻力、滑轮的质量和摩擦均不计)
如图所示,跨过定滑轮的轻绳两端的物体A和B的质量分别为M和m,物体A在光滑水平面上,B由静止释放,当B沿竖直方向下降h时,这时细绳与水平面的夹角为θ,试求(空气阻力、滑轮的质量和摩擦均不计)(1)此时A的速度大小;
(2)B下降h的过程中,绳子拉力所做的功?
分析 (1)B参与两个分运动,沿绳子方向和垂直绳子方向的两个分运动,由于绳子长度一定,故A下降的速度等于B沿绳子方向的分速度,再分别对A、B两个物体,应用系统的机械能守恒列式即可求解.
(2)对B,运用动能定理求解绳子拉力所做的功.
解答 解:(1)把A沿水平面运动的速度v分解为沿绳方向的速度v1和垂直绳方向的速度v2,则v1就是绳的速度,等于B物体的速度,即:
vB=v1=vAcosθ
由系统的机械能守恒得:
mgh=$\frac{1}{2}m{v}_{B}^{2}$+$\frac{1}{2}M{v}_{A}^{2}$
联立解得:vA=$\sqrt{\frac{2mgh}{mco{s}^{2}θ+M}}$
(2)由上得:vB=vAcosθ=cosθ$\sqrt{\frac{2mgh}{mco{s}^{2}θ+M}}$
对B,由动能定理得:
mgh+W=$\frac{1}{2}m{v}_{B}^{2}$
解得绳子拉力所做的功为:W=-$\frac{Mmgh}{mco{s}^{2}θ+M}$
答:(1)此时A的速度大小是$\sqrt{\frac{2mgh}{mco{s}^{2}θ+M}}$;
(2)B下降h的过程中,绳子拉力所做的功为-$\frac{Mmgh}{mco{s}^{2}θ+M}$.
点评 关键要找出合运动和分运动,得到两个物体速度的关系,再根据系统的机械能守恒和动能定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.关于波速公式v=λf,下面哪几句话是正确的( )
| A. | 适用于一切波 | |
| B. | 对同一机械波来说,通过不同的介质时,频率f不变 | |
| C. | 一列绳波的振动频率f变大,λ要减小 | |
| D. | 声音由空气传入水中,f 不变,λ减小 |
8.圆周运动中,对于向心加速度an与r,从an=ω2r看an与r成正比,从an=$\frac{{v}^{2}}{r}$看an与r成反比,那么( )
| A. | an与r成正比不对 | |
| B. | an与r成反比不对 | |
| C. | 两个说法都不对 | |
| D. | 两种说法都对,只是条件不同说法不一样而已 |
12.如图所示,一辆向右行驶的汽车将一重物A匀速提起,在此过程中,说法正确的是( )
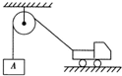

| A. | 汽车向右减速行驶,且车所受地面的支持力增大 | |
| B. | 汽车向右减速行驶,且所受地面摩擦力不变 | |
| C. | 汽车向右匀速行驶,且所受地面摩擦力不变 | |
| D. | 汽车向右匀速行驶,且车所受牵引力减小 |
2.A、B两个物体从同一地点开始在同一直线上做匀变速运动,它们的速度-时间图象如图所示,则( )
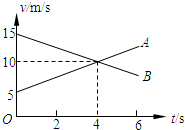

| A. | A、B两个物体的运动方向相反 | B. | t=4s时,两物体相遇 | ||
| C. | t=4s时,两物体距离最小 | D. | 相遇前,两物体最大距离为20m |

 在探究物体的加速度与所受外力、质量的关系实验中,小车及车中的砝码质量用M表示,盘及盘中的砝码质量用m表示.
在探究物体的加速度与所受外力、质量的关系实验中,小车及车中的砝码质量用M表示,盘及盘中的砝码质量用m表示.