Question

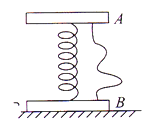
【题目】“太空粒子探测器”是由加速、偏转和收集三部分组成.其原理可简化如下：如图所示，辐射状的加速电场区域边界为两个同心平行半圆弧面，圆心为M，外圆弧面AB与内圆弧面CD的电势差为U.图中偏转磁场分布在以P为圆心，半径为3R的圆周内，磁感应强度大小为B，方向垂直纸面向外；内有半径为R的圆盘（圆心在P处）作为收集粒子的装置，粒子碰到圆盘边缘即被吸收.假设太空中漂浮着质量为m，电量为q的带正电粒子，它们能均匀地吸附到AB圆弧面上，并被加速电场从静止开始加速，从M点以某一速率向右侧各个方向射入偏转磁场，不计粒子间的相互作用和其他星球对粒子引力的影响。

（1）粒子到达M点的速率?

（2）若电势差U=，则粒子从M点到达圆盘的最短时间是多少?

（3）接第（2）问，试求到达圆盘的粒子数与到达M点的粒子总数比值η。（结果用反三角函数表示，例：sinθ=k，则θ=arcsink，θ为弧度）

Answer 1

【答案】（1）；（2）；（3）

【解析】

(1)设粒子到达M点的速度为v，由动能定理：qU=mv2

解得：

v=，

(2)将U=代入，则有：

v==，

设该粒子轨迹半径为r，根据：qvB=m，

解得：

r=2R，

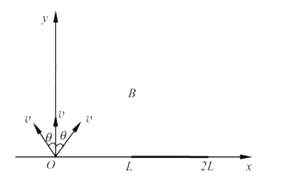
若要时间最短，则粒子在磁场中运动的弦长最短，故从M斜向上射入，到达圆盘的粒子用时最短；如图所示：

由几何关系可得：ME=EO=OM=2R，

故∠MOE=，可得：

tmin=T，

因为：T=，

所以：

tmin=，

(3)若粒子以与MP成α角从M点射入磁场，轨迹恰好与圆盘相切，画出轨迹如图所示；

根据几何关系找出粒子轨迹的圆心与O1刚好落在磁场的边界上，则有：MP=O1P=3R

在等腰MPO1中作PF⊥MO1

因为PF与该粒子从M进入时的速度方向平行，故：

sinα==，

即：

α=arcsin，

若粒子以与MP垂直从M点射入磁场，轨迹也恰与圆盘相切，如图所示；

故入射角度在arcsin至之间的粒子打在圆盘上；

故达圆盘的粒子数与到达M点的粒子总数比值：

η=；