题目内容
(14分)如图所示,绝缘倾斜固定轨道上A点处有一带负电,电量大小q=0.4C质量为0.3kg的小物体,斜面下端B点有一小圆弧刚好与一水平放置的薄板相接,AB点之间的距离S=1.92m,斜面与水平面夹角θ=37°,物体与倾斜轨道部分摩擦因数为0.2,斜面空间内有水平向左,大小为E1=10V/m的匀强电场,现让小物块从A点由静止释放,到达B点后冲上薄板,薄板由新型材料制成,质量M=0.6kg,长度为L,物体与薄板的动摩擦因数μ=0.4,放置在高H=1.6m的光滑平台上,此时,在平台上方虚线空间BCIJ内加上水平向右,大小为E2=1.5V/m的匀强电场,经t=0.5s后,改成另一水平方向的电场E3,在此过程中,薄板一直加速,到达平台右端C点时,物体刚好滑到薄板右端,且与薄板共速,由于C点有一固定障碍物,使薄板立即停止,而小物体则以此速度V水平飞出,恰好能从高h=0.8m的固定斜面顶端D点沿倾角为53°的斜面无碰撞地下滑,(重力加速度g=10m/s2,sin37°= ,cos37°=
,cos37°= )求:
)求:
(1)小物体水平飞出的速度v及斜面距平台的距离X;
(2)小物体运动到B点时的速度VB;
(3)电场E3的大小和方向,及薄板的长度L
(1) 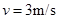
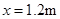 (2)
(2) 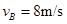 (3)
(3) 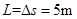
解析试题分析:(1)物体恰好从D点无碰撞飞入,所以有: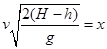 1分
1分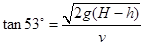 1分 所以解得:
1分 所以解得: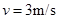
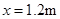 2分
2分
(2)小物体在斜面上运动时,因为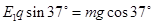 ,所以
,所以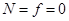 2分 从A到B 过程中,由动能定理知:
2分 从A到B 过程中,由动能定理知: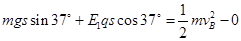 ,解得:
,解得: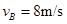 2分
2分
(3)加上E2后,对物块: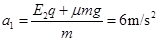
对木板: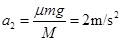
经0.5s后,对物块: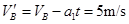
对木板: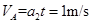
加上E3后,由于木板一直加速,最终为V=3m/s,所以加速时间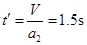 ,所以E3作用了1s,物块由5m/s减速到3m/s用了1s,所以
,所以E3作用了1s,物块由5m/s减速到3m/s用了1s,所以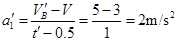 ,又因为
,又因为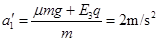 ,解得:
,解得: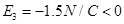 ,即方向向左,所以薄板的长度为
,即方向向左,所以薄板的长度为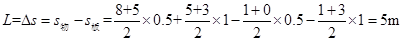
考点:本题考查牛顿运动定律的应用,解答时应从“恰好能从高h=0.8m的固定斜面顶端D点沿倾角为53°的斜面无碰撞地下滑”作为突破口,采取从后往前的分析解答.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
 ;
;

 =0.2,小车足够长。g取10m/s2,求:
=0.2,小车足够长。g取10m/s2,求: