题目内容
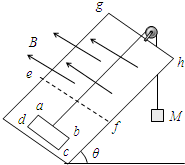
(2011?顺义区一模)如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l
1,bc边的边长为l
2,线框的质量为m,电阻为R,线框通过细棉线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,在进入磁场的这段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
|
|
|
|
分析:由题,线框进入磁场的过程做匀速运动,M的重力势能减小转化为m的重力势能和线框中的内能,根据能量守恒定律求解焦耳热.线框进入磁场前,根据牛顿第二定律求解加速度.由平衡条件求出线框匀速运动的速度,再求出时间.
解答:解:A、线框进入磁场的过程做匀速运动,M的重力势能减小转化为m的重力势能和线框中的内能,根据能量守恒定律得:焦耳热为Q=(Mg-mgsinθ)l
2.故A正确.
B、线框进入磁场前,根据牛顿第二定律得:a=
.故B错误.
C、D设线框匀速运动的速度大小为v,则线框受到的安培力大小为F=
,根据平衡条件得:F=Mg-mgsinθ,联立两式得,v=
,匀速运动的时间为
t=
=
.故CD均错误.
故选A
点评:本题是电磁感应与力平衡的综合,安培力的计算是关键.本题中运用的是整体法求解加速度.
 涓€棰樹竴棰樻壘绛旀瑙f瀽澶參浜�
涓€棰樹竴棰樻壘绛旀瑙f瀽澶參浜�
涓嬭浇浣滀笟绮剧伒鐩存帴鏌ョ湅鏁翠功绛旀瑙f瀽绔嬪嵆涓嬭浇
练习册系列答案
相关题目
 (2011?顺义区一模)如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l1,bc边的边长为l2,线框的质量为m,电阻为R,线框通过细棉线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,在进入磁场的这段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )
(2011?顺义区一模)如图,光滑斜面的倾角为θ,斜面上放置一矩形导体线框abcd,ab边的边长为l1,bc边的边长为l2,线框的质量为m,电阻为R,线框通过细棉线绕过光滑的滑轮与重物相连,重物质量为M,斜面上ef线(ef平行底边)的右方有垂直斜面向上的匀强磁场,磁感应强度为B,如果线框从静止开始运动,在进入磁场的这段时间是做匀速运动的,且线框的ab边始终平行底边,则下列说法正确的是( )

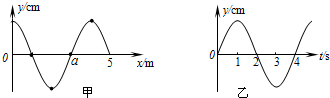 (2011?顺义区一模)一列沿x轴传播的简谐横波某时刻的波形图线如图甲所示,若从此时刻开始计时,图乙是a质点的振动图线,则( )
(2011?顺义区一模)一列沿x轴传播的简谐横波某时刻的波形图线如图甲所示,若从此时刻开始计时,图乙是a质点的振动图线,则( ) (2011?顺义区一模)直线AB是某电场中的一条电线.若有一电子以某一初速度仅在电场力的作用下,沿AB由A运动到B,其速度图象如图所示,下列关于A、B两点的电场强度EA、EB和电势φA、φB的判断正确的是( )
(2011?顺义区一模)直线AB是某电场中的一条电线.若有一电子以某一初速度仅在电场力的作用下,沿AB由A运动到B,其速度图象如图所示,下列关于A、B两点的电场强度EA、EB和电势φA、φB的判断正确的是( )