题目内容
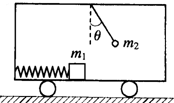在水平地面上运动的小车车厢底部有一质量为m1的木块，木块和车厢通过一根水平轻弹簧相连接，弹簧的劲度系数为k．在车厢的顶部用一根细线悬挂一质量为m2的小球．某段时间内发现细线与竖直方向的夹角为θ，在这段时间内木块与车厢也保持相对静止，如图所示．不计木块与车厢底部的摩擦力，则在这段时间内弹簧的形变量为| m1gtanθ |
| k |
| m1gtanθ |
| k |
分析：物块、小球和小车具有相同的加速度，根据对小球分析，运用牛顿第二定律求出加速度的大小，再对物块分析，根据牛顿第二定律求出弹簧弹力的大小，从而通过胡克定律求出弹簧的形变量．
解答：解：以小球为研究对象，分析受力情况，根据牛顿第二定律得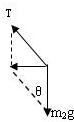
：
m2gtanθ=m2a，得：a=gtanθ
再以质量为m1的木块为研究对象，由牛顿第二定律得
F=m1a
又由胡克定律得：F=kx
解得x=
．
故答案为：
：m2gtanθ=m2a，得：a=gtanθ
再以质量为m1的木块为研究对象，由牛顿第二定律得
F=m1a
又由胡克定律得：F=kx
解得x=
| m1gtanθ |
| k |
故答案为：
| m1gtanθ |
| k |
点评：本题要抓住木块与小球、车的加速度都相同，灵活选择研究对象，采用隔离法处理．
练习册系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
如图所示，粗糙水平地面与半径为R的光滑半圆轨道BCD相连接，且在同一竖直平面内，O是BCD的圆心，BOD在同一竖直线上．质量为m的小物块在水平恒力F的作用下，由静止开始做匀加速直线运动，小物块与水平地面间的动摩擦因数为μ．当小物块运动到B点时撤去F，小物块沿半圆轨道运动恰好能通过D点．求：
（2008?宜宾模拟）如图所示，宽L=1m、高h=7.2m、质量M=8kg的上表面光滑的木板在水平地面上运动，木板与地面间的动摩擦因数μ=0.2．当木板的速度为vo=3m/s时，把一质量m=2kg的光滑小铁块（可视为质点）无初速轻放在木板上表面的右端，取g=10m/s2．求：
、
，分别以初速度
和
迎面相向运动，他们与地面的滑动摩擦系数均为
，当两电动小车间的距离为
时，同时关闭两电动小车的电源，经一定时间后两电动小车相碰．求：
，则碰撞过程中电动小车1受到的撞击力约为多大？
