题目内容
【题目】如图所示,所有轨道均光滑,轨道AB与水平面的夹角为θ=37°,A点距水平轨道的高度为H=1.8m.一无动力小滑车质量为m=1.0kg,从A点沿轨道由静止滑下,经过水平轨道BC再滑入圆形轨道内侧,圆形轨道半径R=0.5m,通过圆形轨道最高点D然后从水平轨道E点飞出,E点右侧有一壕沟,E、F两点的竖直高度差h=1.25m,水平距离s=2.6m.不计小滑车通过B点时的能量损失,小滑车在运动全过程中可视为质点,g=10m/s2,sin37°=0.6,cos37°=0.8,求:
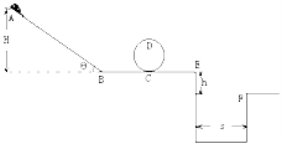
(1)小滑车从A滑到B所经历的时间;
(2)在圆形轨道最高点D处小滑车对轨道的压力大小;
(3)要使小滑车既能安全通过圆形轨道又不掉进壕沟,则小滑车至少应从离水平轨道多高的地方由静止滑下.
【答案】(1)1s (2)22N(3)1.352m
【解析】
试题分析:(1)滑块在斜面的加速度由牛顿第二定律可得:a=gsinθ
AB之间的距离为:![]()
由位移公式得:x=![]() at2
at2
代入数据解得:t=1s
(2)小滑车由A到D过程由动能定理得:mg(H-2R)= ![]() mvD2
mvD2
在D点由牛顿第二定律有:![]()
代入数据解得FN=22N
由牛顿第三定律知小滑车对轨道的压力为22N
(3)小滑车要能安全通过圆形轨道,在平台上速度至少为v1,
则由动能定理得: ![]() mvD2+mg(2R)=
mvD2+mg(2R)= ![]() mv12
mv12
由重力提供向心力有:![]()
小滑车要能越过壕沟,小滑车做平抛,在平台上速度至少为v2,则
竖直方向上:h=![]() gt2
gt2
水平方向上:s=v2t
因为v2>v1,所以只要mgH=![]() mv22
mv22
代入数据联立解得:H=1.352m

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目