Question

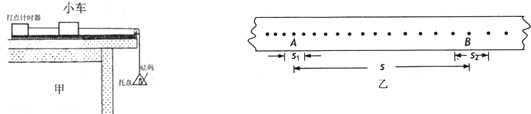
在“探究恒力做功与动能改变的关系”实验中，某同学采用如图所示装置进行探究，实验中他用钩码的重力来表示小车受到的合外力，为了减小采用这种方案所带来的实验误差．你认为他应该采取的两项必要措施是：
a．

平衡摩擦力

；
b．

小车的总质量远大于钩码质量

．

Answer 1

分析：a．小车在水平木板运动时水平方向上受到绳的拉力和摩擦力，想用钩码的重力表示小车受到的合外力，首先需要平衡摩擦力；
b．设小车加速度为a，则：绳上的力为F=Ma，对钩码来说：mg-Ma=ma，即：mg=（M+m）a，如果用钩码的重力表示小车受到的合外力，则Ma=（M+m）a，必须要满足钩码的质量远小于小车的总质量．

解答：解：a．车在水平木板运动时水平方向受到绳的拉力和摩擦力，想用钩码的重力表示小车受到的合外力，首先需要平衡摩擦力；
b、设小车质量M，钩码质量m，整体的加速度为a，绳上的拉力为F，则：
对小车有：F=Ma；
对钩码有：mg-F=ma，即：mg=（M+m）a；
如果用钩码的重力表示小车受到的合外力，则要求：Ma=（M+m）a，必须要满足小车的总质量远大于钩码质量，这样两者才能近似相等．
故答案为：
a．平衡摩擦力
b．小车的总质量远大于钩码质量

点评：要明确此题在验证合外力的功与动能变化间的关系中用到的原理，围绕原理，可与探究牛顿第二定律的实验结合学习．