题目内容
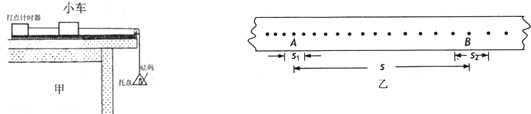
在探究“恒力做功与动能改变的关系”的实验中,某同学采用如下图装置,小车质量M,在平衡摩擦力之后,挂上重物m后,小车拖动纸带并打出一系列的点.图中的纸带只是打出的纸带的一部分,所标注的点相邻两点的时间间隔为T.使用毫米刻度尺进行测量后,将数据记录在图中.则:(重力加速度为g)

(1)若在该实验装置中绳子对小车的拉力取为mg,则小车质量M与所挂重物质量m应满足什么关系
A、M>m B、M>>m C、M<m D、M<<m
(2)若小车质量M和重物质量m满足(1)中条件,请用题目所给各个物理量的符号计算下面问题:
b点所对应的小车运动的动能为
;
从b点到e点,小车动能的增加量为
;
从b点到e点,重物对小车做功

(1)若在该实验装置中绳子对小车的拉力取为mg,则小车质量M与所挂重物质量m应满足什么关系
B
B
A、M>m B、M>>m C、M<m D、M<<m
(2)若小车质量M和重物质量m满足(1)中条件,请用题目所给各个物理量的符号计算下面问题:
b点所对应的小车运动的动能为
| M(s1+s2)2 |
| 8T2 |
| M(s1+s2)2 |
| 8T2 |
从b点到e点,小车动能的增加量为
| M[(s4+s5)2-(s1+s2)2] |
| 8T2 |
| M[(s4+s5)2-(s1+s2)2] |
| 8T2 |
从b点到e点,重物对小车做功
mg(s2+s3+s4)
mg(s2+s3+s4)
.分析:(1)重物加速下滑,处于失重状态,其对细线的拉力小于重力,要使其对细线的拉力近似等于重力,应该使加速度减小,即重物的质量应该远小于小车的质量;
(2)对纸带处理得到B点和E点的速度,进一步得到动能的增加量.重物的重力近似等于细线的拉力,根据功的定义,可知从b点到e点重物对小车做功.
(2)对纸带处理得到B点和E点的速度,进一步得到动能的增加量.重物的重力近似等于细线的拉力,根据功的定义,可知从b点到e点重物对小车做功.
解答:解:(1)重物加速下滑,处于失重状态,其对细线的拉力小于重力,设拉力为T,根据牛顿第二定律,有
对重物,有 mg-T=ma
对小车,有 T=Ma
解得
T=
mg
故当M>>m时,有T≈mg
故:M>>m.
(2)小车做匀加速直线运动,纸带上任意一点的速度等于该点前后相邻两点间的平均速度,
故b点速度为:vb=
,e点速度为:ve=
,
故b点所对应的小车运动的动能为为Ekb=
Mvb2=
M(
)2=
从b点到e点,小车动能的增加量为△Ek=Eke-Ekb=
Mve2-
Mvb2=
M(
)2-
M(
)2=
重物的重力近似等于细线的拉力,根据功的定义,从b点到e点,重物对小车做功:W=mg(s2+s3+s4)
故答案为:(1)B (2)
、
、mg(s2+s3+s4).
对重物,有 mg-T=ma
对小车,有 T=Ma
解得
T=
| M |
| M+m |
故当M>>m时,有T≈mg
故:M>>m.
(2)小车做匀加速直线运动,纸带上任意一点的速度等于该点前后相邻两点间的平均速度,
故b点速度为:vb=
| s1+s2 |
| 2T |
| s4+s5 |
| 2T |
故b点所对应的小车运动的动能为为Ekb=
| 1 |
| 2 |
| 1 |
| 2 |
| s1+s2 |
| 2T |
| M(s1+s2)2 |
| 8T2 |
从b点到e点,小车动能的增加量为△Ek=Eke-Ekb=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| s4+s5 |
| 2T |
| 1 |
| 2 |
| s1+s2 |
| 2T |
| M[(s4+s5)2-(s1+s2)2] |
| 8T2 |
重物的重力近似等于细线的拉力,根据功的定义,从b点到e点,重物对小车做功:W=mg(s2+s3+s4)
故答案为:(1)B (2)
| M(s1+s2)2 |
| 8T2 |
| M[(s4+s5)2-(s1+s2)2] |
| 8T2 |
点评:本题关键是根据实验原理并结合牛顿第二定律和动能定理来确定要测量的量、实验的具体操作方法和实验误差的减小方法.

练习册系列答案
相关题目
 在探究“恒力做功与动能改变的关系”的实验中,某同学用1kg的小车,在平衡摩擦力之后,挂上40g的小砂桶后,小车拖动纸带并打出一系列的点.图中的纸带只是打出的纸带的一部分,所标注的点是计时器每打5点所取的一个计数点,测量数据如图.则:(所用交流电的频率为50Hz,重力加速度g=9.80m/s2)
在探究“恒力做功与动能改变的关系”的实验中,某同学用1kg的小车,在平衡摩擦力之后,挂上40g的小砂桶后,小车拖动纸带并打出一系列的点.图中的纸带只是打出的纸带的一部分,所标注的点是计时器每打5点所取的一个计数点,测量数据如图.则:(所用交流电的频率为50Hz,重力加速度g=9.80m/s2)