题目内容
 如图所示,可看成质点的A、B两个木块的质量均为2kg,两个木块与水平地面之间的滑动摩擦系数均为0.2,两木块之间用长为1m、质量不计的细线连接,放在水平地面上,在大小为10N的水平拉力F作用下一起向右运动,则此时A、B两个木块向右运动的加速度大小为
如图所示,可看成质点的A、B两个木块的质量均为2kg,两个木块与水平地面之间的滑动摩擦系数均为0.2,两木块之间用长为1m、质量不计的细线连接,放在水平地面上,在大小为10N的水平拉力F作用下一起向右运动,则此时A、B两个木块向右运动的加速度大小为0.5
0.5
m/s2.若细线在两木块向右运动的速度为8m/s时断裂,则在细线断裂后的5s末,A、B两木块之间的距离为61.5
61.5
m.分析:以AB整体受力分析,利用牛顿第二定律列式求解即可求出加速度;断裂后,B做匀减速直线运动,A继续做匀加速直线运动,求出加速度,利用时间位移公式即可求解.
解答: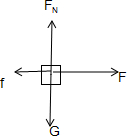 解:AB整体受力分析如图所示:
解:AB整体受力分析如图所示:
由牛顿第二定律得:F-μ(mA+mB)g=(mA+mB)a
代入数据得:a=0.5m/s2
由公式v2=2ax得:
绳断前两物体运动的位移:x1=
=
m=64m
绳断后对B由牛顿第二定律得:
aB=
=μg=2m/s2
停下来所用时间:
t0=
=
s=4s<5s
即4s末到5s末B处于静止状态,
B减速位移xB=
t0=
×4m=16m
绳断后对A由牛顿第二定律得:aA=
=3m/s2
5s内A运动的位移为:
xA=vt+
aAt2
=8×5+
×3×52m
=77.5m
在细线断裂后的5s末,A、B两木块之间的距离为△x=xA-xB=77.5-16m=61.5m
故答案为:0.5,61.5
 解:AB整体受力分析如图所示:
解:AB整体受力分析如图所示:由牛顿第二定律得:F-μ(mA+mB)g=(mA+mB)a
代入数据得:a=0.5m/s2
由公式v2=2ax得:
绳断前两物体运动的位移:x1=
| v2 |
| 2a |
| 82 |
| 2×0.5 |
绳断后对B由牛顿第二定律得:
aB=
| μmBg |
| mB |
停下来所用时间:
t0=
| v |
| aB |
| 8 |
| 2 |
即4s末到5s末B处于静止状态,
B减速位移xB=
| v |
| 2 |
| 8 |
| 2 |
绳断后对A由牛顿第二定律得:aA=
| F-μmAg |
| mA |
5s内A运动的位移为:
xA=vt+
| 1 |
| 2 |
=8×5+
| 1 |
| 2 |
=77.5m
在细线断裂后的5s末,A、B两木块之间的距离为△x=xA-xB=77.5-16m=61.5m
故答案为:0.5,61.5
点评:本题属于已知受力求运动,关键是能够正确地受力分析,根据牛顿第二定律求解出加速度,然后合力选择运动学公式求解.

练习册系列答案
相关题目

 (2011?西乡县模拟)如图所示,某重型汽车的额定牵引力的功率为160kW,汽车质量为5t,车长为L=8m,平板车厢距地面高为h=1.8m,如图所示,可看成质点的木箱质量为1000kg,静止停放在平板车厢最前方.为了验证汽车的性能,司机以额定功率由静止启动,此时木箱与车厢出现相对滑动,2s后脱离车厢,已知木箱与车厢动摩擦因数μ=0.1,汽车所受地面阻力等于其对地面压力的k倍,其中k=0.1,g取10m/s2.试求:
(2011?西乡县模拟)如图所示,某重型汽车的额定牵引力的功率为160kW,汽车质量为5t,车长为L=8m,平板车厢距地面高为h=1.8m,如图所示,可看成质点的木箱质量为1000kg,静止停放在平板车厢最前方.为了验证汽车的性能,司机以额定功率由静止启动,此时木箱与车厢出现相对滑动,2s后脱离车厢,已知木箱与车厢动摩擦因数μ=0.1,汽车所受地面阻力等于其对地面压力的k倍,其中k=0.1,g取10m/s2.试求:
