题目内容
小球从空中A点竖直上抛,下落过程落到距A点正下方h处C点的速度恰好是下落到距A点正上方h处B点的速度的2倍,则小球上升过程所能达到的最高点O距A点的高度是( )
分析:设小球初速度为v0,运动到B点的速度大小为v,则运动到C点速度大小为2v,对从A到B和从A到C两个过程运用动能定理求出初速度,再根据竖直上抛速度位移公式即可求解.
解答:解:设小球初速度为v0,运动到B点的速度大小为v,则运动到C点速度大小为2v,
从A到B的过程运用动能定理得:
mv2-
mv02=-mgh①
从A到C的过程运用动能定理得:
m(2v)2-
mv02=mgh②
由①②解得:v02=
gh
设上升的最大高度为H,则有:
H=
=
h
故选B
从A到B的过程运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
从A到C的过程运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
由①②解得:v02=
| 10 |
| 3 |
设上升的最大高度为H,则有:
H=
| v02 |
| 2g |
| 5 |
| 3 |
故选B
点评:本题主要考查了动能定理和竖直上抛运动位移速度公式的直接应用,难度不大,属于基础题.

练习册系列答案
相关题目
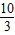 h
h h
h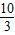 h
h h
h