题目内容
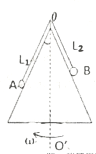
【题目】如图,两个相同的小球A、B用两根轻绳连接后放置在圆锥筒光滑侧面的不同位置上,绳子上端固定在同一点O,连接A球的绳子比连接B球的绳子长,两根绳子都与圆锥筒最靠近的母线平行。当圆锥筒绕其处于竖直方向上的对称轴OO以角速度![]() 匀速转动时,A、B两球都处于筒侧面上与筒保持相对静止随筒转动,下列说法正确的是( )
匀速转动时,A、B两球都处于筒侧面上与筒保持相对静止随筒转动,下列说法正确的是( )
A. 两球所受的合力大小相同
B. A球对绳子的拉力大小等于B球对绳子的拉力大小
C. 两球所需的向心力都等于绳子拉力的水平分力
D. A球对圆锥筒的压力小于B球对圆锥筒的压力
【答案】D
【解析】
A项:设圆锥筒顶角一半为![]() ,则两球做匀速圆周运动的半径分别为:
,则两球做匀速圆周运动的半径分别为:![]() ,
,![]() ,两球所受的合力提供向心力即
,两球所受的合力提供向心力即![]() ,由半径不同,所以两球的合外力大小不相同,故A错误;
,由半径不同,所以两球的合外力大小不相同,故A错误;
B、D项:小球受重力G,支持力N,拉力,水平方向由牛顿第二定律可得:
![]()
竖直方向由平衡条件可得:![]()
解得:![]() ,
,
![]()
由于半径不同,所以两球对细绳的拉力则不同,故B错误,
由于A球圆周运动的半径的半径大于B球做圆周运动的半径,所以A球对圆锥筒的压力小于B球对圆锥筒的压力,故D正确;
C项:两球所需的向心力都等于绳子拉力的水平分力与圆锥筒对小球支持力沿水平方向分力的合力,故C错误。

【题目】一个小球沿斜面向下运动,用每间隔1/10s曝光一次的频闪相机拍摄不同时刻小球位置的照片,如图所示,即照片上出现的相邻两个小球的像之间的时间间隔为1/10s,测得小球在几个连续相等时间内位移(数据见下表),则
s1 | s2 | s3 | s4 |
8.20cm | 9.30cm | 10.40cm | 11.50cm |
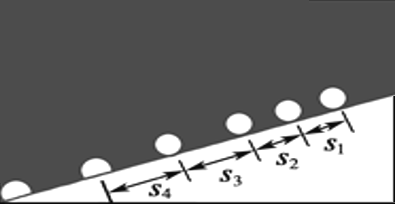
(1)小球在相邻的相等时间内的位移差_____(填“相等”或“不相等”),小球的运动性质属_____直线运动。
(2)有甲、乙两同学计算小球加速度方法如下:
甲同学:![]() ,
,![]() ,
,![]() ;
;
乙同学:![]() ,
,![]() ,
,![]() 。
。
你认为甲、乙中_________同学计算方法更科学?加速度值为________。(结果保留两位有效数字)