题目内容
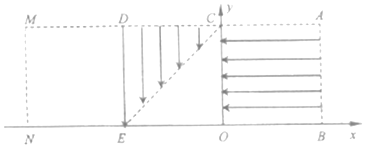
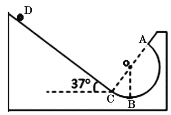
【题目】如图所示，竖直面内有足够长的粗糙斜面，与水平面的夹角为
，斜面下端与半径
的光滑半圆形轨道平滑相连（DC垂直于直径AC），连接点为C，半圆形轨道最低点为B、最高点为A。现将一质量
的小球从斜面上的D点由静止释放，小球会通过A点落回斜面。小球与斜面的摩擦因数=
。已知
，
，当地的重力加速度为
。求：
（1）若DC=9m，小球到达B点时对轨道的压力大小。
（2）若小球过C点后受一个水平向左的恒定外力F=3N，要使小球仍能通过A点，DC的长度应满足什么条件？
（3）若小球过C点后不受水平恒力F。要使小球第一次落回斜面时能够垂直撞击斜面，则小球经过A点的速度为多大？撞击点距C点多远？
【答案】(1)20N（2）
(3)0.75m
【解析】
（1）小球由D到B阶段：
在B点对小球有：
由牛顿第三定律有，小球对轨道的压力大小为
解得：
（2）DC长度为S恰好能过A点
恒力F与重力的合力为：
小球由D到A过程中：
在A点：
解得：S=15.625m
即DC≥15.625m
（3）小球在A点速度为v时，能垂直撞击斜面，设小球从A到斜面用时t
沿斜面方向：
垂直斜面方向：
撞击点到C的距离为x：
解得：v=3m/s
x=0.75m
练习册系列答案
阶梯计算系列答案
相关题目
