Question

（1）氢原子从能级A跃迁到能级B吸收波长为λ₁的光子，从能级A跃迁到能级C吸收波长为λ₂的光子，若λ₂＞λ₁，则当它从能级B跃迁到能级C时，将

 

（选填“吸收”或“放出”）波长为

 

的光子．
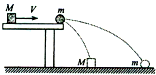
（2）如图，一质量为m的小球静止在光滑水平桌面的边缘，质量为M（M＞m）的小物块以水平速度V运动到桌边与小球相碰，碰后小球与物块落到水平地面上，其落地点与桌面边缘的水平距离之比为x_m：x_M=9：1，已知碰撞时间极短且无动能损失，碰撞前后物块、小球在同一条直线上运动，求小球质量m与物块质量M的比值．

Answer 1

分析：（1）根据玻尔理论知：原子从能级A跃迁到能级B吸收波长为λ₁的光子，说明能级A能量低于能级B．从能级A跃迁到能级C吸收波长为λ₂的光子，说明能级A高于能级C，可知BC能级的关系，判断放出还是吸收光子．并由玻尔理论求出波长．
（2）物块与小球碰撞过程无动能损失，动量和动能均守恒，可得到碰后两者的速度表达式．碰撞后，物块和小球均做平抛运动，由平抛运动规律得到初速度的关系，即可求出质量之比．

解答：解：（1）原子从能级A跃迁到能级B吸收波长为λ₁的光子，说明能级A能量低于能级B．从能级A跃迁到能级C吸收波长为λ₂的光子，说明能级A低于能级C，λ₂＞λ₁，h

c

λ1

＞h

c

λ2

，则可知B能级高于能级C，根据玻尔理论得知，氢原子从能级B跃迁到能级C时，将放出光子．
由玻尔理论得
   E_B-E_A=h

c

λ1

，E_C-E_A=h

c

λ2

，
设氢原子从能级B跃迁到能级C时放出的光子波长为λ，则
    E_B-E_C=h

c

λ

由以上三式得  λ=

λ1λ2

λ2-λ1

（2）取水平向右为正方向，对于碰撞过程，由动量守恒和动能守恒得
   MV=mv+MV′
 

1

2

MV2=

1

2

mv2+

1

2

MV′2
解得  v=

2M

M+m

V，V′=

M-m

M+m

V
碰撞后，物块和小球均做平抛运动，则有
   h=

1

2

gt2
  x_m=vt，
  x_M=V′t
联立解得，m：M=7：9
故答案为：（1）放出，

λ1λ2

λ2-λ1

；（2）小球质量m与物块质量M的比值是7：9．

点评：对于氢原子能级是原子物理部分的重点，要加强练习，牢固掌握．对于含有碰撞的过程，分析物理过程是基础，同时，要抓住弹性碰撞两大基本规律：动量守恒和动能守恒．