题目内容
【题目】某同学设计了一个如图所示的游乐模型，高度为R的竖直圆筒轨道衔接一个半径为2R的四分之一圆形内轨，在圆筒的底部安装一个由高强度弹簧构成的弹射装置，此装置在很短的时间内能把安全囊(包括在里面的游人)以一定的速度弹出，使安全囊从圆内轨的最高点P水平飞出，接着飞入如图所示的缓冲装置。安全囊质量为m(当作质点)，缓冲装置的纵截面可以看作由两个斜面AB、CD和一段光滑圆弧BC组成，安全囊与斜面间的动摩擦因数为0.25，两斜面的倾角θ均为37°，AB＝CD＝2R，A、D等高，D端固定一小挡板，与其碰撞不损失机械能。安全囊始终在同一个竖直平面内运动，重力加速度为g，圆筒轨道和圆形内轨均不计摩擦，sin 37°＝0.6，cos 37°＝0.8。
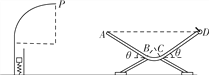
(1)如果安全囊恰好能经P点飞出，且恰好沿AB斜面进入缓冲装置，应调节缓冲装置底部支架高度使斜面的A点（D点）距地面的高度为多少？
(2)接(1)问，假设高强度弹簧构成的弹射装置行程很小，可以认为是零，即安全囊离开地面时的起点高度近似为零，则弹射装置至少需要具有多少弹性势能？
(3)接(1)问，试通过计算描述安全囊进入缓冲装置后的运动过程．
【答案】(1)
R (2)4mgR (3)略
【解析】（1）在P点安全囊只受到重力的作用，重力恰好提供向心力，则：
得P点的速度： 
安全囊到达A时速度的方向沿沿AB的方向，则：vy＝vptanθ＝0.75
所以A、D点距离对面的高度：
；
（2）在P点安全囊的机械能为：E=EP+EK=
mvP2+mg3R=4mgR
由机械能守恒定律即知弹簧的弹性势能：E弹=4mgR
（3）在A点时安全囊的速度
假设经过一个来回能够回到A点，设再次回到A点时的动能为E′k
则E′k＝mv2－μmgcos θ·8R<0
所以安全囊不会滑到A而飞出，最终在B、C间来回滑动
