题目内容
11.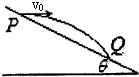 如图所示,宇航员站在某质量分布均匀的星球表面的一斜坡上,从P点以v0水平抛出一个小球,测得小球经时间t落到斜坡上的另一点Q,已知斜坡倾角为θ,该星球的半径为R,万有引力常量为G,求:
如图所示,宇航员站在某质量分布均匀的星球表面的一斜坡上,从P点以v0水平抛出一个小球,测得小球经时间t落到斜坡上的另一点Q,已知斜坡倾角为θ,该星球的半径为R,万有引力常量为G,求:(1)该星球表面的重力加速度g;
(2)该星球的密度ρ.
分析 (1)根据平抛运动水平位移和竖直位移的关系,结合运动学公式求出星球表面的重力加速度.
(2)根据万有引力等于重力求出星球的质量,结合密度公式求出星球的密度.
解答 解:(1)根据$tanθ=\frac{y}{x}=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$ 得:星球表面的重力加速度g=$\frac{2{v}_{0}tanθ}{t}$.
(2)根据万有引力等于重力得,$G\frac{Mm}{{R}^{2}}=mg$,
解得:M=$\frac{g{R}^{2}}{G}$=$\frac{2{v}_{0}{R}^{2}tanθ}{Gt}$.
则星球的密度$ρ=\frac{M}{V}$=$\frac{\frac{2{v}_{0}{R}^{2}tanθ}{Gt}}{\frac{4π{R}^{3}}{3}}$=$\frac{3{v}_{0}tanθ}{2πRtG}$.
答:(1)该星球表面的重力加速度g为$\frac{2{v}_{0}tanθ}{t}$;
(2)该星球的密度ρ为$\frac{3{v}_{0}tanθ}{2πRtG}$.
点评 本题考查了万有引力定律和平抛运动的综合运用,通过平抛运动规律求出星球表面重力加速度是解决本题的关键.

练习册系列答案
相关题目
2.以下关于物质的微观解释正确的是( )
| A. | 气体对容器的压强是大量气体分子对容器的碰撞引起的,它跟气体的重力无关 | |
| B. | 用气筒给自行车打气,越打越费劲,是气体分子之间斥力变大 | |
| C. | 由于液体分子的热运动,液体会表现出各向同性 | |
| D. | 非晶体的微观结构跟液体非常相似,非晶体会表现出各向同性 | |
| E. | 由于多晶体是由许多单晶体杂乱无章地组合而成,所以多晶体各向异性 |
19.如图,横坐标是时间,下列说法正确的是( )


| A. | 若纵坐标表示位移,图象中物体一定做匀速直线运动 | |
| B. | 若纵坐标表示速度,图象中物体一定做匀速直线运动 | |
| C. | 若纵坐标表示位移,图象中物体一定做加速直线运动 | |
| D. | 若纵坐标表示速度,图象中直线的斜率是物体的运动速度 |
6. 竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )
竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )
 竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )
竖直半圆形轨道ACB的半径为R,AB水平,C为轨道最低点,一个小球从A点以速度v0水平抛出,设重力加速度为g,不计空气阻力,则( )| A. | 总可以找到一个v0值,使小球垂直撞击AC段某处 | |
| B. | 总可以找到一个v0值,使小球垂直撞击最低点C | |
| C. | 总可以找到一个v0值,使小球垂直撞击CB段某处 | |
| D. | 无论v0取何值,小球都不可能垂直撞击轨道 |
16. 2016年CCTV-1综合频道在黄金时间播出了电视剧《陆军一号》,其中直升机抢救伤员的情境深深感动了观众.假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,若不计空气阻力,则( )
2016年CCTV-1综合频道在黄金时间播出了电视剧《陆军一号》,其中直升机抢救伤员的情境深深感动了观众.假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,若不计空气阻力,则( )
 2016年CCTV-1综合频道在黄金时间播出了电视剧《陆军一号》,其中直升机抢救伤员的情境深深感动了观众.假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,若不计空气阻力,则( )
2016年CCTV-1综合频道在黄金时间播出了电视剧《陆军一号》,其中直升机抢救伤员的情境深深感动了观众.假设直升机放下绳索吊起伤员后(如图甲所示),竖直方向的速度图象和水平方向的位移图象分别如图乙、丙所示,若不计空气阻力,则( )| A. | 伤员一直处于失重状态 | |
| B. | 绳索中拉力方向一定沿竖直向上 | |
| C. | 地面上观察到伤员的运动轨迹是一条倾斜向上的直线 | |
| D. | 绳索中拉力先大于重力,后小于重力 |
3. 将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
 将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )
将小球以10m/s的初速度从地面竖直向上抛出,取地面为零势能面,小球在上升过程中的动能Ek、重力势能Ep与上升高度h间的关系分别如图中两直线所示.取g=10m/s2,下列说法正确的是( )| A. | 小球的质量为0.2 kg | |
| B. | 小球受到的阻力(不包括重力)大小为0.20 N | |
| C. | 小球动能与重力势能相等时的高度为$\frac{20}{13}$ m | |
| D. | 小球上升到2 m时,动能与重力势能之差为0.5 J |
20. 物体从O点出发,沿水平直线运动,取向右的方向为运动的正方向,其v-t图如图所示,则物体在最初的4s内是( )
物体从O点出发,沿水平直线运动,取向右的方向为运动的正方向,其v-t图如图所示,则物体在最初的4s内是( )
 物体从O点出发,沿水平直线运动,取向右的方向为运动的正方向,其v-t图如图所示,则物体在最初的4s内是( )
物体从O点出发,沿水平直线运动,取向右的方向为运动的正方向,其v-t图如图所示,则物体在最初的4s内是( )| A. | 物体做匀变速直线运动,加速度方向始终向右 | |
| B. | 物体始终向右运动 | |
| C. | 前2s物体在O点的左边,后2s在O点的右边 | |
| D. | t=2s时刻,物体与O点距离最远 |
 如图所示,真空中有Q=8.0×10-5C的点电荷,在距离r=2.0cm的A位置有一电荷量q=+1.0×10-9C的检验电荷.已知静电力常量k=9.0×109N•m2/C2.求:
如图所示,真空中有Q=8.0×10-5C的点电荷,在距离r=2.0cm的A位置有一电荷量q=+1.0×10-9C的检验电荷.已知静电力常量k=9.0×109N•m2/C2.求: