题目内容
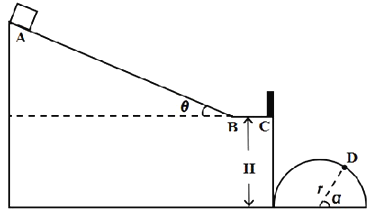
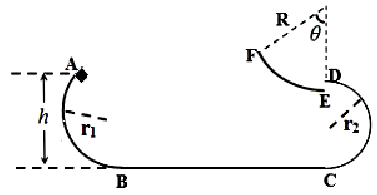
【题目】如图所示，半径
的圆弧轨道AB 与水平轨道BC 相切于B 点，CD为r2 = 0．40m 的半圆轨道，另一半径R=1．00m 的圆弧轨道EF 与CD 靠近，E 点略低于D 点。一质量m=1kg 的小物块（可视为质点）从A 点以初速度v0=2m/s 沿轨道下滑，在AB 段运动过程中始终受到竖直向上F＝10N 的力作用，进入BC 段后撤去。已知AB 高度为h，BC 长L=1．00m，小物块与BC 间动摩擦因数μ=0．2，其余光滑，EF 轨道对应的圆心角θ＝60°，所有轨道均固定在同一竖直平面内，不考虑小物块在各轨道相接处的能量损失，忽略空气阻力，g 取10m/s2，求：
（1）当小物块在圆弧轨道AB 运动到B 点时，轨道对小物块的作用力大小；
（2）若小物块在B 点的速度为5m/s，且在刚进入BC 段时撤去力F，请通过计算判断小物块能否通过D 点；
（3）若小物块能进入EF 轨道，且不越过F 点，小物块在D 点的速度范围是多少？
【答案】（1）10+5
N；（2）能通过D 点；（3）
m/s
【解析】
试题分析：AB段由于外力不做功，速度大小不变，方向改变，求到B点时轨道对小物块的作用力大小，考查的是向心力。从B点到D点，摩擦力做功，重力做功，可以运用动能定理；而要使小球能够通过D点，需要的最小速度又考查了向心力公式。EF轨道光滑，机械能守恒。
（1）由于F竖直向上，大小等于重力，所以AB段合外力作功为零，VB=V0=2 m/s
设在B点轨道对小物块作用力为FB
FB-mg=
FB=10+5N
（2）如能通过D点，根据动能定理：
-
-mg2r2=
MVD2-MVB2
VD=4 m/s >
=2 m/s
所以小物块能通过D 点。
（3）通过D 点的最小速度为=2 m/s
如刚好到达F点，则在D点的速度VD，
m VD，2=mg（R-Rcos
）
VD，= m/s
所以小物块在D点的速度范围2 m/s
VD
m/s
