Question

【题目】消防车的供水系统主要由水泵、输水管道和水炮组成。如图所示，消防水炮离地高度为H＝80 m，建筑物上的火点离地高度为h＝60 m，整个供水系统的效率η＝60%（供水效率η定义为单位时间内抽水过程水所获得的机械能与水泵功率的比值×100%）。假设水从水炮水平射出，水炮的出水速度v0＝30 m/s，水炮单位时间内的出水量m0＝60 kg/s，取g＝10 m/s2，不计空气阻力。

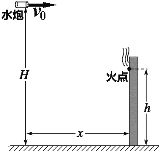
（1）求水炮与火点的水平距离x，和水炮与火点之间的水柱的质量m；

（2）若认为水泵到炮口的距离也为H＝80 m，求水泵的功率P；

（3）如图所示，为流速稳定分布、体积不可压缩且粘性可忽略不计的液体（比如水）中的一小段液柱，由于体积在运动中不变，因此当S1面以速度v1向前运动了x1时，S2面以速度v2向前运动了x2，若该液柱前后两个截面处的压强分别为p1和p2，选用恰当的功能关系证明：流速稳定分布、体积不可压缩且粘性可忽略不计的液体水平流动（或者高度差的影响不显著）时，液体内流速大的地方压强反而小。

Answer 1

【答案】(1) 120kg (2) 1.25×102 kW (3)见解析；

【解析】

(1)根据平抛运动规律，有

H－h＝gt2 ①

x＝v0t ②

联立上述两式，并代入数据得

t=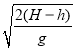＝2 s

x＝v0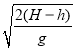＝60 m ③

水炮与火点之间的水柱的质量

m= m0t=120kg ④

(2)设在Δt时间内出水质量为Δm，则Δm= m0Δt，由功能关系得：

⑤

即

解得：

P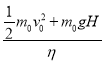＝＝1.25×102 kW ⑥

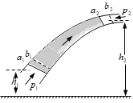
(3)表示一个细管，其中流体由左向右流动。在管的a1处和a2处用横截面截出一段流体，即a1处和a2处之间的流体，作为研究对象。

a1处的横截面积为S1，流速为v1，高度为h1，a1处左边的流体对研究对象的压强为p1，方向垂直于S1向右。

a2处的横截面积为S2，流速为v2，高度为h2，a2处左边的流体对研究对象的压强为p2，方向垂直于S2向左。

经过很短的时间间隔Δt，这段流体的左端S1由a1移到b1。右端S2由a2移到b2。两端移动的距离分别为Δl1和Δl2。左端流入的流体体积为ΔV1=S1Δl1，右端流出的流体体积为ΔV2=S2Δl2，理想流体是不可压缩的，流入和流出的体积相等，ΔV1=ΔV2，记为ΔV。

现在考虑左右两端的力对这段流体所做的功。

作用在液体左端的力F1=p1S1向右，所做的功

W1=F1Δl1=(p1S1)Δl1=p1(S1Δl1) =p1ΔV。

作用在液体右端的力F2=p2S2向左，所做的功

W2=－F2Δl2=－(p2S2)Δl2=－p2(S2Δl2) =－p2ΔV。

外力所做的总功

W= W1＋W2=(p1－p2)ΔV ①

外力做功使这段流体的机械能发生改变。初状态的机械能是a1处和a2处之间的这段流体的机械能E1，末状态的机械能是b1处和b2处之间的这段流体的机械能E2。由b1到a2这一段，经过时间Δt，虽然流体有所更换，但由于我们研究的是理想流体的定常流动，流体的密度ρ和各点的流速v没有改变，动能和重力势能都没有改变，所以这一段的机械能没有改变，这样机械能的改变(E2－E1)就等于流出的那部分流体的机械能减去流入的那部分流体的机械能。

由于m=ρΔV，所以流入的那部分流体的动能为

重力势能为

mgh1＝ρΔVgh1

流出的那部分流体的动能为

重力势能为

mgh2＝ρΔVgh2

机械能的改变为

②

理想流体没有粘滞性，流体在流动中机械能不会转化为内能，所以这段流体两端受的力所做的总功W等于机械能的改变，即

W=E2－E1 ③

将①式和②式代入③式，得

④

整理后得

⑤

a1和a2是在流体中任意取的，所以上式可表示为对管中流体的任意处：

（常量）⑥

④式和⑤式称为伯努利方程。

流体水平流动时，或者高度差的影响不显著时（如气体的流动），伯努利方程可表达为

（常量）⑦

从⑥式可知，在流动的流体中，压强跟流速有关，流速v大的地方要强p小，流速v小的地方压强p大。