Question

【题目】如图所示，长L=9m的传送带与水平方向的倾角为37°，在电动机的带动下以v=4m/s的速率顺时针方向运行，在传送带的B端有一离传送带很近的挡板P可将传送带上的物块挡住，在传送带的A端无初速地放一质量m=1kg的物块，它与传送带间的动摩擦因数μ=0.5。物块与挡板碰撞时间忽略不计，物块与挡板的碰撞中能量损失也不计。若g=10m/s2，则下列说法中正确的是( )

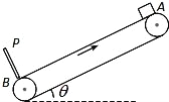
A. 物块从静止释放到第一次下滑到挡板P处所用的时间为3s

B. 物块从静止释放到第一次下滑到挡板P处的过程中，物块相对传送

带滑行的路程为9m

C. 物块从静止释放下滑到底端和挡板碰撞后还能再上滑至原来出发点

D. 物块从静止释放到第一次上升至最高点的过程中，物块与传送带间摩擦生热为100.8J

Answer 1

【答案】AD

【解析】

物块从A点由静止释放，物块相对传送带向下滑，物块沿传送带向下加速运动的加速度a1；根据牛顿第二定律有：mgsinθμmgcosθ＝m a1得：a1＝gsinθμgcosθ＝2m/s2；由L＝at2得物块从A到B的时间，选项A正确；在此过程中物块相对传送带移动的路程为s1＝L+vt1＝21m，选项B错误；与P碰前的速度，挡板碰撞后，以v1的速度反弹，因v1＞v，物块相对传送带向上滑，物块向上做减速运动的加速度为a2；根据牛顿第二定律，有mgsinθ+μmgcosθ＝ma2得a2＝gsinθ+μgcosθ＝10m/s2；物块速度减小到与传送带速度相等的时间；在t2时间内物块向上的位移；物块相对传送带向上的位移；与传送带速度相等后物块相对传送带向下滑，物块向上做减速运动的加速度a3；根据牛顿第二定律，有mgsinθμmgcosθ＝ma3得a3＝2m/s2；物块速度减小到零的时间t3＝v/a3＝2s；物块向上的位移； 此过程中物块相对传送带向下的位移；因L1+L2=5m<L=9m，可知物块不能再上滑至原来出发点，选项C错误；物块从静止释放到第一次上升至最高点的过程中，物块与传送带间摩擦生热为，选项D正确；故选AD.