题目内容
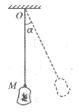
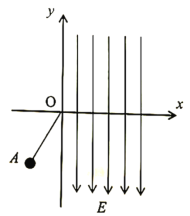
【题目】如图,xoy直角坐标系构成一竖直平面,其第一、四象限范围内(含y轴)存在方向竖直向下、场强大小E=4.5×103N/C的匀强电场。一个质量m=1.0kg、带电量q=-4×10-3C的小球(可视为质点),用长度l=1.0m的不可伸长的绝缘轻绳悬挂在原点O处。现将小球向左拉至坐标为(-0.6m,-0.8m)的A点处静止释放,绳始终未被拉断,g取10m/s2。求小球:
(1)从A点第一次运动到y轴处时的速度大小;
(2)第一次从y轴向右运动,经过与A点等高处位置的横坐标;
(3)第一次离开电场前瞬间绳子受到的拉力大小。
【答案】(1)2m/s(2)![]() m(3)40N
m(3)40N
【解析】
(1)设从A点运动到O点时的速度为v0,A运动到O点过程,由机械能守恒定律得:
![]()
解得:
![]() ;
;
(2)小球所受电场力为:
F=qE=4×103×4.5×103=18N
小球刚进入电场时做圆周运动的向心力:
![]()
因
Fmg=8N>Fn
小球做类平抛运动,第一次向右运动到与A点等高处过程,y方向上有:
![]()
![]()
得:
![]()
x方向:
![]()
即横坐标为![]() ;
;
(3)当线刚拉直时由:
![]()
解得:
t=0.5s
此时有:
x=v0t2=1.0m
![]()
即小球刚好在圆心等高处绳子拉直,而后做圆周运动,此时小球向上的速度为:
v1=at2=4m/s
设小球运动到最高点速度为v2,由动能定理得:
![]()
代入数据解得:
![]()
此时,由牛顿第二定律得:
![]()
解得:
T=40N

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目