题目内容
如图甲所示,直角坐标系中直线AB与横轴x夹角∠BAO=30°,AO长为a.假设在点A处有一放射源可沿∠BAO所夹范围内的各个方向放射出质量为m、速度大小均为v、带电量为e的电子,电子重力忽略不计.在三角形ABO内有垂直纸面向里的匀强磁场,当电子从顶点A沿AB方向射入磁场时,电子恰好从O点射出.试求:①从顶点A沿AB方向射入的电子在磁场中的运动时间t;
②磁场大小、方向保持不变,改变匀强磁场分布区域,使磁场存在于三角形ABO内的左侧,要使放射出的电子穿过磁场后都垂直穿过y轴后向右运动,试求匀强磁场区域分布的最小面积S.
③磁场大小、方向保持不变,现改变匀强磁场分布区域,使磁场存在于y轴与虚线之间,示意图见图乙所示,仍使放射出的电子最后都垂直穿过y轴后向右运动,试确定匀强磁场左侧边界虚线的曲线方程.

【答案】分析:(1)粒子做圆周运动,根据粒子在磁场中运动的半径公式和周期公式可以求得粒子的运动的时间;
(2)以AB方向发射的电子在磁场中的运动轨迹与AO中垂线交点的左侧圆弧,有界磁场的上边界:以A点正上方、距A点的距离为a的点为圆心,以a为半径的圆弧.
(3)根据所有的电子最后都垂直穿过y轴后向右运动,做出电子的运动的轨迹,根据几何关系可以求得左侧边界虚线的曲线方程.
解答:解:(1)根据题意,电子在磁场中的运动的轨道半径R=a,
由evB=
得:B=
由T=
t= =
=
(2)有界磁场的上边界:
以AB方向发射的电子在磁场中的运动轨迹与AO中垂线交点的左侧圆弧
有界磁场的上边界:以A点正上方、距A点的距离为a的点为圆心,以a为半径的圆弧.
故最小磁场区域面积为:
(3)设在坐标(x,y)的点进入磁场,
由相似三角形得到:
圆的方程为:x2+(y+b)2=a2
消去(y+b),磁场边界的方程为: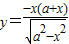

点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.
(2)以AB方向发射的电子在磁场中的运动轨迹与AO中垂线交点的左侧圆弧,有界磁场的上边界:以A点正上方、距A点的距离为a的点为圆心,以a为半径的圆弧.
(3)根据所有的电子最后都垂直穿过y轴后向右运动,做出电子的运动的轨迹,根据几何关系可以求得左侧边界虚线的曲线方程.
解答:解:(1)根据题意,电子在磁场中的运动的轨道半径R=a,
由evB=

得:B=

由T=

t=
 =
=
(2)有界磁场的上边界:
以AB方向发射的电子在磁场中的运动轨迹与AO中垂线交点的左侧圆弧
有界磁场的上边界:以A点正上方、距A点的距离为a的点为圆心,以a为半径的圆弧.
故最小磁场区域面积为:

(3)设在坐标(x,y)的点进入磁场,
由相似三角形得到:

圆的方程为:x2+(y+b)2=a2
消去(y+b),磁场边界的方程为:
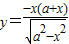

点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

 绕O点在Oxy平面内匀速转动,在它旋转一圈后的过程中(从图示位置开始计时)它的感应电动势与时间的关系图线是图乙中哪一个? ( )
绕O点在Oxy平面内匀速转动,在它旋转一圈后的过程中(从图示位置开始计时)它的感应电动势与时间的关系图线是图乙中哪一个? ( )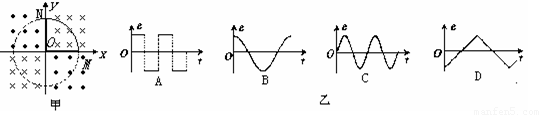
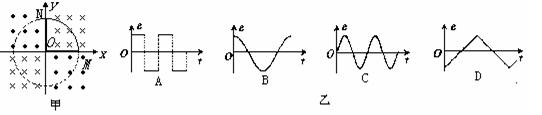
 绕O点在Oxy平面内匀速转动,在它旋转一圈后的过程中(从图示位置开始计时)它的感应电动势与时间的关系图线是图乙中哪一个? ( )
绕O点在Oxy平面内匀速转动,在它旋转一圈后的过程中(从图示位置开始计时)它的感应电动势与时间的关系图线是图乙中哪一个? ( )