题目内容
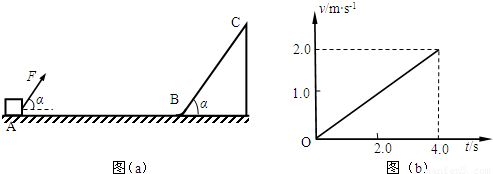
足够长光滑斜面BC的倾角α=53°,小物块与水平面间的动摩擦因数为0.5,水平面与斜面之间B点有一小段弧形连接,一质量m=2kg的小物块静止于A点.现在AB段对小物块施加与水平方向成α=53°的恒力F作用,如图(a)所示,小物块在AB段运动的速度-时间图象如图(b)所示,到达B点迅速撤去恒力F.(已知sin53°=0.8,cos53°=0.6).求:(1)小物块所受到的恒力F;
(2)小物块从B点沿斜面向上运动,到返回B点所用的时间;
(3)小物块能否返回到A点?若能,计算小物块通过A点时的速度;若不能,计算小物块停止运动时离B点的距离.
【答案】分析:(1)根据v-t图象得到运动情况,结合速度时间关系公式求解加速度;然后对物体受力分析,并根据牛顿第二定律列式求解拉力F;
(2)先受力分析并根据牛顿第二定律求解加速度,然后根据速度时间关系公式求解;
(3)对小物块从B向A运动过程中,求解出最大位移后比较,即可得到结论.
解答:解:(1)由图(b)可知,AB段加速度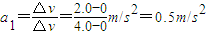
根据牛顿第二定律,有Fcosα-μ(mg-Fsinα)=ma
得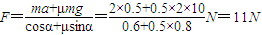
(2)在BC段mgsinα=ma2
解得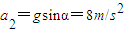
小物块从B到C所用时间与从C到B所用时间相等,有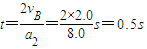
(3)小物块从B向A运动过程中,有μmg=ma3
解得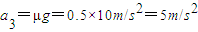
滑行的位移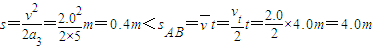
所以小物块不能返回到A点,停止运动时,离B点的距离为0.4m.
答:(1)小物块所受到的恒力F为11N;
(2)小物块从B点沿斜面向上运动,到返回B点所用的时间为0.5s;
(3)小物块不能返回到A点,停止运动时,离B点的距离为4m.
点评:本题是已知运动情况确定受力情况和一直受力情况确定运动情况的问题,关键求解出加速度,然后根据运动学公式列式求解.
(2)先受力分析并根据牛顿第二定律求解加速度,然后根据速度时间关系公式求解;
(3)对小物块从B向A运动过程中,求解出最大位移后比较,即可得到结论.
解答:解:(1)由图(b)可知,AB段加速度
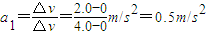
根据牛顿第二定律,有Fcosα-μ(mg-Fsinα)=ma
得
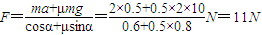
(2)在BC段mgsinα=ma2
解得
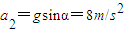
小物块从B到C所用时间与从C到B所用时间相等,有
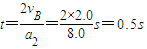
(3)小物块从B向A运动过程中,有μmg=ma3
解得
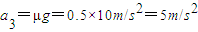
滑行的位移
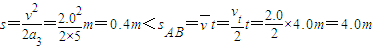
所以小物块不能返回到A点,停止运动时,离B点的距离为0.4m.
答:(1)小物块所受到的恒力F为11N;
(2)小物块从B点沿斜面向上运动,到返回B点所用的时间为0.5s;
(3)小物块不能返回到A点,停止运动时,离B点的距离为4m.
点评:本题是已知运动情况确定受力情况和一直受力情况确定运动情况的问题,关键求解出加速度,然后根据运动学公式列式求解.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目




