题目内容

足够长光滑斜面BC的倾角α＝53º，小物块与水平面间的动摩擦因数为0.5，水平面与斜面之间B点有一小段弧形连接，一质量m=2kg的小物块静止于A点。现在AB段对小物块施加与水平方向成α＝53º的恒力F作用，如图（a）所示，小物块在AB段运动的速度－时间图像如图（b）所示，到达B点迅速撤去恒力F。（已知sin53º＝0.8，cos53º＝0.6）。求：

（1）小物块所受到的恒力F；
（2）小物块从B点沿斜面向上运动，到返回B点所用的时间；
（3）小物块能否返回到A点？若能，计算小物块通过A点时的速度；若不能，计算小物块停止运动时离B点的距离。

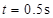（1）（2）（3）小物块不能返回到A点，停止运动时，离B点的距离为0.4m。

解析试题分析：
解：（1）由图（b）可知，AB段加速度
根据牛顿第二定律，有
得
（2）在BC段

小物块从B到C所用时间与从C到B所用时间相等，有

（3）小物块从B向A运动过程中，有

滑行的位移
所以小物块不能返回到A点，停止运动时，离B点的距离为0.4m。
考点：牛顿第二定律；匀变速直线运动的位移与时间的关系．
点评：本题是牛顿第二定律和运动学的综合应用，注意结合图像处理问题．