题目内容
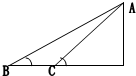
如图AB、AC两个粗糙斜面等高，倾角θ1＞θ2，一物体从静止开始由A点沿AB下滑过程中的加速度为a1，抵达B点的速度为V1；此物体由A点沿AC下滑过程中加速度为a2，抵达C点的速度为V2，设物体与每个面的摩擦系数相同．则（ ）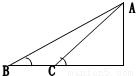
A．a1＜a2，V1＜V2
B．a1＜a2，V1＞V2
C．a1＞a2，V1＞V2
D．a1＞a2，V1＜V2
【答案】分析：根据牛顿第二定律求出物体沿斜面下滑的加速度大小，根据速度位移公式求出到达底端的速度大小，从而比较大小，
解答：解：根据牛顿第二定律得，
=gsinθ2-μgcosθ2，同理a2=gsinθ1-μgcosθ1，因为θ1＞θ2，所以a1＜a2．
根据速度位移公式得，在AB面上滑动时，
，解得
，同理解得
，因为hcotθ2＞hcotθ1，则v1＜v2．故A正确，B、C、D错误．
故选A．
点评：本题考查了牛顿第二定律和运动学公式的综合运用，知道加速度是联系力学和运动学的桥梁．
解答：解：根据牛顿第二定律得，
=gsinθ2-μgcosθ2，同理a2=gsinθ1-μgcosθ1，因为θ1＞θ2，所以a1＜a2．根据速度位移公式得，在AB面上滑动时，
，解得，同理解得，因为hcotθ2＞hcotθ1，则v1＜v2．故A正确，B、C、D错误．故选A．
点评：本题考查了牛顿第二定律和运动学公式的综合运用，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，两个物体A和B由同一地点出发沿同一直线向同一方向运动的v-t图象运动过程中，A、B的运动情况为（ ）
如图AB、AC两个粗糙斜面等高，倾角θ1＞θ2，一物体从静止开始由A点沿AB下滑过程中的加速度为a1，抵达B点的速度为V1；此物体由A点沿AC下滑过程中加速度为a2，抵达C点的速度为V2，设物体与每个面的摩擦系数相同．则（ ）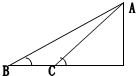
如图AB、AC两个粗糙斜面等高，倾角θ1＞θ2，一物体从静止开始由A点沿AB下滑过程中的加速度为a1，抵达B点的速度为V1；此物体由A点沿AC下滑过程中加速度为a2，抵达C点的速度为V2，设物体与每个面的摩擦系数相同．则