题目内容
如图AB、AC两个粗糙斜面等高,倾角θ1>θ2,一物体从静止开始由A点沿AB下滑过程中的加速度为a1,抵达B点的速度为V1;此物体由A点沿AC下滑过程中加速度为a2,抵达C点的速度为V2,设物体与每个面的摩擦系数相同.则( )
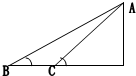
| A.a1<a2,V1<V2 | B.a1<a2,V1>V2 |
| C.a1>a2,V1>V2 | D.a1>a2,V1<V2 |

根据牛顿第二定律得,a1=
=gsinθ2-μgcosθ2,同理a2=gsinθ1-μgcosθ1,因为θ1>θ2,所以a1<a2.
根据速度位移公式得,在AB面上滑动时,v12=2a1
,解得v1=
,同理解得v2=
,因为hcotθ2>hcotθ1,则v1<v2.故A正确,B、C、D错误.
故选A.
| mgsinθ2-μmgcosθ2 |
| m |
根据速度位移公式得,在AB面上滑动时,v12=2a1
| h |
| sinθ2 |
| 2gh-2μghcotθ2 |
| 2gh-2μghcotθ1 |
故选A.

练习册系列答案
相关题目
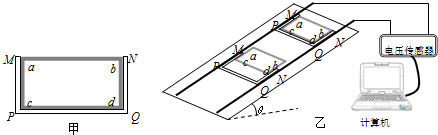

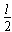 、ab= cd=l,方框外侧套着一个内侧壁长分别为
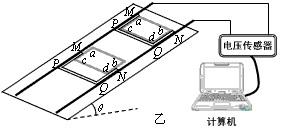
、ab= cd=l,方框外侧套着一个内侧壁长分别为 及l的U型金属框架MNPQ(下面简称U型框),U型框与方框之间接触良好且无摩擦。两个金属框的质量均为m,PQ边、ab边和cd边的电阻均为r,其余各边电阻可忽略不计。将两框放于静止在水平地面上的矩形粗糙绝缘平面上,将平面的一端缓慢抬起,直到这两框都恰能在此平面上匀速下滑,这时平面与地面的夹角为θ,此时将平面固定构成一个倾角为θ的斜面。已知两框与斜面间的最大静摩擦力近似等于滑动摩擦力。在斜面上有两条与其底边垂直的、电阻可忽略不计,且足够长的光滑金属轨道,两轨道间的宽度略大于l,使两轨道能与U型框保持良好接触,在轨道上端接有电压传感器并与计算机相连,如图乙所示。在轨道所在空间存在垂直于轨道平面斜向下、磁感强度大小为B的匀强磁场。
及l的U型金属框架MNPQ(下面简称U型框),U型框与方框之间接触良好且无摩擦。两个金属框的质量均为m,PQ边、ab边和cd边的电阻均为r,其余各边电阻可忽略不计。将两框放于静止在水平地面上的矩形粗糙绝缘平面上,将平面的一端缓慢抬起,直到这两框都恰能在此平面上匀速下滑,这时平面与地面的夹角为θ,此时将平面固定构成一个倾角为θ的斜面。已知两框与斜面间的最大静摩擦力近似等于滑动摩擦力。在斜面上有两条与其底边垂直的、电阻可忽略不计,且足够长的光滑金属轨道,两轨道间的宽度略大于l,使两轨道能与U型框保持良好接触,在轨道上端接有电压传感器并与计算机相连,如图乙所示。在轨道所在空间存在垂直于轨道平面斜向下、磁感强度大小为B的匀强磁场。 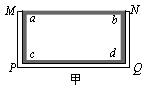


 、ab=cd=l,方框外侧套着一个内侧壁长分别为
、ab=cd=l,方框外侧套着一个内侧壁长分别为 及l的U型金属框架MNPQ(下面简称U型框),U型框与方框之间接触良好且无摩擦.两个金属框的质量均为m,PQ边、ab边和cd边的电阻均为r,其余各边电阻可忽略不计.将两个金属框放在静止在水平地面上的矩形粗糙绝缘平面上,将平面的一端缓慢抬起,直到这两个金属框都恰能在此平面上匀速下滑,这时平面与地面的夹角为θ,此时将平面固定构成一个倾角为θ的斜面.已知两框与斜面间的最大静摩擦力近似等于滑动摩擦力.在斜面上有两条与其底边垂直的、电阻可忽略不计,且足够长的光滑金属轨道,两轨道间的宽度略大于l,使两轨道能与U型框保持良好接触,在轨道上端接有电压传感器并与计算机相连,如图乙所示.在轨道所在空间存在垂直于轨道平面斜向下、磁感强度大小为B的匀强磁场.
及l的U型金属框架MNPQ(下面简称U型框),U型框与方框之间接触良好且无摩擦.两个金属框的质量均为m,PQ边、ab边和cd边的电阻均为r,其余各边电阻可忽略不计.将两个金属框放在静止在水平地面上的矩形粗糙绝缘平面上,将平面的一端缓慢抬起,直到这两个金属框都恰能在此平面上匀速下滑,这时平面与地面的夹角为θ,此时将平面固定构成一个倾角为θ的斜面.已知两框与斜面间的最大静摩擦力近似等于滑动摩擦力.在斜面上有两条与其底边垂直的、电阻可忽略不计,且足够长的光滑金属轨道,两轨道间的宽度略大于l,使两轨道能与U型框保持良好接触,在轨道上端接有电压传感器并与计算机相连,如图乙所示.在轨道所在空间存在垂直于轨道平面斜向下、磁感强度大小为B的匀强磁场.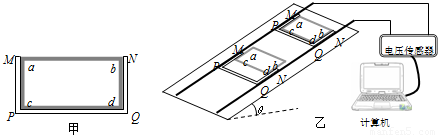
 的电源;若串联在一起,可等效为电动势为2E,内电阻为2r的电源.
的电源;若串联在一起,可等效为电动势为2E,内电阻为2r的电源.