题目内容
12.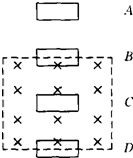 如图所示,矩形线圈由位置A开始下落,如果在磁场中受到的磁场力总是小于重力,则它通过A,B,C,D四个位置时(B,D位置恰使线圈面积有一半在磁场中),加速度的关系为( )
如图所示,矩形线圈由位置A开始下落,如果在磁场中受到的磁场力总是小于重力,则它通过A,B,C,D四个位置时(B,D位置恰使线圈面积有一半在磁场中),加速度的关系为( )| A. | aA>aB>aC>aD | B. | aA=aC>aB>aD | C. | aA=aC>aD>aB | D. | aA=aC>aB=aD |
分析 线圈自由下落时,加速度为g.线圈进入和穿出磁场过程中,切割磁感线产生感应电流,将受到向上的安培力.线圈完全在磁场中时,不产生感应电流,线圈只受重力,加速度等于g.根据牛顿第二定律分析加速度的关系.
解答 解:线圈自由下落时,加速度为aA=g.线圈完全在磁场中时,磁通量不变,不产生感应电流,线圈不受安培力作用,只受重力,加速度为aC=g.
线圈进入和穿出磁场过程中,切割磁感线产生感应电流,将受到向上的安培力,根据牛顿第二定律得知,aB<g,aD<g.线圈完全在磁场中时做匀加速运动,到达D处的速度大于B处的速度,则线圈在D处所受的安培力大于在B处所受的安培力,又知,磁场力总小于重力,则aB>aD,故aA=aC>aB>aD.故B正确,ACD错误.
故选:B.
点评 本题关键是分析安培力的大小和方向情况,抓住安培力大小与速度成正比,分析B、D两处安培力的大小关系,同时注意将得出的加速度与重力加速度相比较更为容易得出加速度的大小关系.

练习册系列答案
相关题目
1.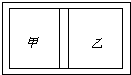 如图所示,用导热的固定隔板把一容器隔成体积相等的甲、乙两部分.甲、乙中分别有质量相等的氮气和氧气.在达到平衡时,它们的温度相等.若分子势能可忽略,则甲、乙中( )
如图所示,用导热的固定隔板把一容器隔成体积相等的甲、乙两部分.甲、乙中分别有质量相等的氮气和氧气.在达到平衡时,它们的温度相等.若分子势能可忽略,则甲、乙中( )
 如图所示,用导热的固定隔板把一容器隔成体积相等的甲、乙两部分.甲、乙中分别有质量相等的氮气和氧气.在达到平衡时,它们的温度相等.若分子势能可忽略,则甲、乙中( )
如图所示,用导热的固定隔板把一容器隔成体积相等的甲、乙两部分.甲、乙中分别有质量相等的氮气和氧气.在达到平衡时,它们的温度相等.若分子势能可忽略,则甲、乙中( )| A. | 气体的压强相等 | B. | 气体的内能相等 | ||
| C. | 气体分子的平均动能相等 | D. | 气体分子的平均速率相等 |
2.物体做下列几种运动,其机械能一定守恒的运动是( )
| A. | 平抛运动 | B. | 匀加速向上直线运动 | ||
| C. | 匀加速向下直线运动 | D. | 在竖直平面内做匀速圆周运动 |
19.关于重力势能的变化,下列说法中正确的是( )
| A. | 物体受拉力和重力作用向上运动,拉力做功是1J,物体重力势能的增加量也为1J | |
| B. | 从同一高度将一某物体以相同的速率平抛或斜抛,落到地面上时,物体重力势能的变化一定不相同 | |
| C. | 从同一高度落下的物体到达地面,考虑空气阻力和不考虑空气阻力的情况下,重力势能的减少量一定相同 | |
| D. | 物体运动中重力做功是-1J,但物体重力势能的增加量不一定是1J |
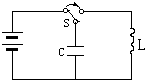
7.如图所示为LC振荡电路,当开关S打向右边发生振荡后,下列说法中正确的是( )

| A. | 振荡电流达到最大值时,电容器上的带电量为零 | |
| B. | 振荡电流达到最大值时,磁场能最大 | |
| C. | 振荡电流为零时,电场能为零 | |
| D. | 振荡电流相邻两次为零的时间间隔等于振荡周期的一半 |
17. 如图上表面为光滑圆柱形曲面的物体静置于水平地面上,一小滑块从曲面底端受水平力作用缓缓地沿曲面向上滑动一小段的过程中物体始终静止不动,则地面对物体的摩擦力f和地面对物体的支持力N大小变化的情况是( )
如图上表面为光滑圆柱形曲面的物体静置于水平地面上,一小滑块从曲面底端受水平力作用缓缓地沿曲面向上滑动一小段的过程中物体始终静止不动,则地面对物体的摩擦力f和地面对物体的支持力N大小变化的情况是( )
 如图上表面为光滑圆柱形曲面的物体静置于水平地面上,一小滑块从曲面底端受水平力作用缓缓地沿曲面向上滑动一小段的过程中物体始终静止不动,则地面对物体的摩擦力f和地面对物体的支持力N大小变化的情况是( )
如图上表面为光滑圆柱形曲面的物体静置于水平地面上,一小滑块从曲面底端受水平力作用缓缓地沿曲面向上滑动一小段的过程中物体始终静止不动,则地面对物体的摩擦力f和地面对物体的支持力N大小变化的情况是( )| A. | f增大,N减小 | B. | f增大,N不变 | C. | f不变,N不变 | D. | f减小,N增大 |
1.某同学利用橡皮条将模型飞机弹出,在弹出过程中,下述说法中不正确的是( )
| A. | 弹力对飞机做正功 | B. | 飞机的动能增加 | ||
| C. | 橡皮条的弹性势能减少 | D. | 飞机的重力势能转化为飞机的动能 |
2.如图所示为甲、乙两物体从同一地点沿直线向同一方向运动的v-t图象,则( )
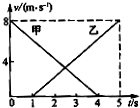

| A. | 甲、乙两物体在4s末相距最远 | |
| B. | 甲、乙两物体在4s末相遇λ | |
| C. | 前4s内甲物体的速度总是大于乙的速度 | |
| D. | 甲、乙两物体在2.5s末相距最远 |