题目内容
1.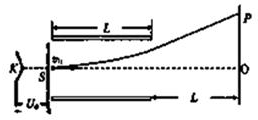 如图所示,水平放置的两块金属板长为L,两块间距为d,两板间电压为U,且上板为正,金属板右边缘到屏的距离为L,电极K发出的电子(初速度不计)经加速电场加速后,由小孔S以速度v0沿水平金属板间的中心线射入板间,并最终打在屏幕上的P点,电子质量m、带电量为e,电子重力不计,求:
如图所示,水平放置的两块金属板长为L,两块间距为d,两板间电压为U,且上板为正,金属板右边缘到屏的距离为L,电极K发出的电子(初速度不计)经加速电场加速后,由小孔S以速度v0沿水平金属板间的中心线射入板间,并最终打在屏幕上的P点,电子质量m、带电量为e,电子重力不计,求:(1)加速电压U0的大小;
(2)电子飞出电场时的速度v的大小;
(3)OP的长度l.
分析 (1)对直线加速过程,根据动能定理列式求解加速电压;
(2)对类似平抛运动,根据分运动公式列式求解,最后合成得到末速度;
(3)对类似平抛运动,根据分运动公式列式求解速度偏转角的正切值tanθ;然后结合几何关系求解PO的长度l.
解答 解:(1)对直线加速过程,根据动能定理,有:
eU0=$\frac{1}{2}m{v}_{0}^{2}$
解得:${U}_{0}=\frac{m{v}_{0}^{2}}{2e}$
(2)对类平抛运动的过程,有:
L=v0t
vx=v0
vy=at
其中:a=$\frac{eU}{md}$
合速度:v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$
联立解得:v=$\sqrt{{v}_{0}^{2}+{(\frac{eUL}{md{v}_{0}})}^{2}}$
(3)类似平抛运动过程的速度偏转角的正切值为:
tanθ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{eUL}{md{v}_{0}^{2}}$ 结合几何关系,有:
结合几何关系,有:
l=($\frac{L}{2}+L$)tanθ=$\frac{3eU{L}^{2}}{2md{v}_{0}^{2}}$
答:(1)加速电压U0的大小为$\frac{m{v}_{0}^{2}}{2e}$;
(2)电子飞出电场时的速度v的大小为$\sqrt{{v}_{0}^{2}+{(\frac{eUL}{md{v}_{0}})}^{2}}$;
(3)OP的长度l为$\frac{3eU{L}^{2}}{2md{v}_{0}^{2}}$.
点评 本题关键是明确粒子的运动情况和受力情况,分为直线加速过程、类似平抛运动过程和匀速直线运动过程进行分析讨论,不难.

练习册系列答案
相关题目
11.下列四个单位中,是电场强度E的单位的是( )
| A. | N/C | B. | C/kg | C. | V•m | D. | N•m2/C2 |
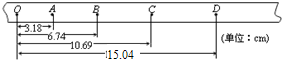
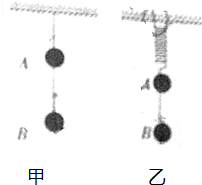 (1)如图甲所示,A.B间用细绳联结并将A球用轻绳悬挂在天花版上,剪断悬挂A球的细线的瞬间,A,B的加速度分别为多大?
(1)如图甲所示,A.B间用细绳联结并将A球用轻绳悬挂在天花版上,剪断悬挂A球的细线的瞬间,A,B的加速度分别为多大?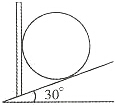 在倾角为30°的斜而上有一块竖直放置的挡板,在挡板和斜面之间放置一个重20N的光滑小球,如图所示.试求这个球对斜面的压力和对挡板的压力.
在倾角为30°的斜而上有一块竖直放置的挡板,在挡板和斜面之间放置一个重20N的光滑小球,如图所示.试求这个球对斜面的压力和对挡板的压力.
 如图所示,工人师傅推动一台重300N的割草机,施加力F的大小为100N,方向斜向下与水平方向成α=37°角(sin 37°=0.6,cos 37°=0.8).
如图所示,工人师傅推动一台重300N的割草机,施加力F的大小为100N,方向斜向下与水平方向成α=37°角(sin 37°=0.6,cos 37°=0.8).