Question

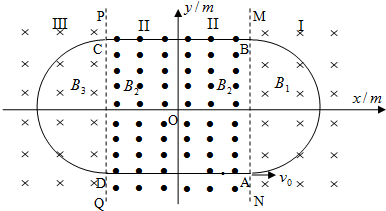
在竖直平面内建立xoy直角坐标系，oy表示竖直向上方向．如图所示．已知该平面内存在沿x轴正向的区域足够大的匀强电场．一带电小球从坐标原点o沿oy方向以4J的初动能竖直向上抛出．不计空气阻力，它到达的最高位置如图中M点所示．

求：
（1）小球在M点时的动能E_kM．
（2）设小球落回跟抛出点在同一水平面时的位置为N，求小球到达N点时的动能E_kN．

Answer 1

分析：解答本题要抓住：
1．水平受Eq向右，一直做初速度为0的匀加速直线运动，竖直受mg向下，做竖直上抛运动，互不影响．
2．竖直上升到最高点的时间等于从最高点落回抛出高度的时间．
3．根据竖直上抛和匀加速直线运动的特点即可解题．

解答：解：（1）在竖直方向小球只受重力，从O→M速度由v₀减小到0；
在水平方向小球只受电场力F，速度由0增大到v₁；
由图知这两个分运动相等时间内的位移之比为：y₁：x₁=4：3
所以平均速度大小之比为4：3，因此v₀：v₁=4：3，
所以

EKM

EK0

=

1 2 mv12

1 2 mv02

=

9

16

解得：小球在M点时的动能E_KM=2.25J．
（2）由竖直分运动知，O→M和M→N经历的时间相同，因此水平位移大小之比为x₁：x₂=1：3，故N点的横坐标为12．
小球到达N点时的竖直分速度为v₀，水平分速度为2v₁，所以N点水平方向的动能为：E_kNx=

1

2

m(2v1)2=4EKM=9J
由此可得此时动能E_kN=4+9J=13J．
答：（1）小球在M点时的动能为2.25J；
（2）小球到达N点时的动能为13J．

点评：本题主要注意不一定求动能就把速度求出来，有时只需要知道速度之比即可，难度适中．