题目内容
4.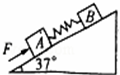 质量相等的两物体A和B,用轻弹簧连接后放在粗糙面上,A、B与斜面间动摩擦因数相同.对A施加沿斜面向上的推力F,使A、B相对静止地沿斜面向上运动,此时弹簧长度为L1,撤去拉力F,换成大小仍为F的沿斜面向上拉力拉B,A、B保持相对静止后弹簧长度为L2,下列判断正确的是( )
质量相等的两物体A和B,用轻弹簧连接后放在粗糙面上,A、B与斜面间动摩擦因数相同.对A施加沿斜面向上的推力F,使A、B相对静止地沿斜面向上运动,此时弹簧长度为L1,撤去拉力F,换成大小仍为F的沿斜面向上拉力拉B,A、B保持相对静止后弹簧长度为L2,下列判断正确的是( )| A. | 两种情况下A、B保持相对静止后弹簧的长度相等 | |
| B. | 两种情况下A、B保持相对静止后两物块的加速度不相等 | |
| C. | 弹簧的原长为$\frac{{L}_{1}+{L}_{2}}{2}$ | |
| D. | 弹簧的劲度系数为$\frac{F}{{L}_{2}+{L}_{1}}$ |
分析 对整体分析,根据牛顿第二定律求出整体的加速度,分别对第一种情况的A和第二种情况的B分析,运用牛顿第二定律联立求出弹簧的原长和劲度系数.从而求出弹簧的形变量.
解答 解:BCD:以A、B为整体,根据牛顿第二定律知,两种情况下的加速度相等,设A的质量为m,则加速度为:
a=$\frac{F}{2m}$-gsinθ-μgcosθ,
设弹簧的原长为l0,根据牛顿第二定律,
第一种情况:对A,k(L1-L0)-mgsinθ-μmgcosθ=ma…①
第二种情况:对B,k(L0-L2)-mgsinθ-μ•mgcosθ=ma…②
由①②得:L0=$\frac{{L}_{1}+{L}_{2}}{2}$,
劲度系数为:k=$\frac{F}{{L}_{1}-{L}_{2}}$;
故BD错误,C正确.
A、第一种情况弹簧的形变量为△L=L1-L0=$\frac{{L}_{1}-{L}_{2}}{2}$,
第二种情况弹簧的形变量△L=L0-L2=$\frac{{L}_{1}-{L}_{2}}{2}$.故两种情况下形变量相同,但长度不相同,故A错误;
故选:C.
点评 本题考查了牛顿第二定律和胡克定律的综合运用,关键选择好研究的对象,运用牛顿第二定律进行求解,掌握整体法和隔离法的运用.

练习册系列答案
相关题目
14.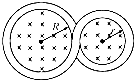 由一段外皮绝缘的导线扭成如图所示的闭合回路,大圆的半径为R,小圆的半径为r.且R>r.两圆形区域内有方向垂直平面向里、磁感应强度大小为B的匀强磁场,下列判断正确的是( )
由一段外皮绝缘的导线扭成如图所示的闭合回路,大圆的半径为R,小圆的半径为r.且R>r.两圆形区域内有方向垂直平面向里、磁感应强度大小为B的匀强磁场,下列判断正确的是( )
 由一段外皮绝缘的导线扭成如图所示的闭合回路,大圆的半径为R,小圆的半径为r.且R>r.两圆形区域内有方向垂直平面向里、磁感应强度大小为B的匀强磁场,下列判断正确的是( )
由一段外皮绝缘的导线扭成如图所示的闭合回路,大圆的半径为R,小圆的半径为r.且R>r.两圆形区域内有方向垂直平面向里、磁感应强度大小为B的匀强磁场,下列判断正确的是( )| A. | 穿过该闭合回路的磁通量的大小为Bπ(R2-r2) | |
| B. | 穿过该闭合回路的磁通量的大小为Bπ(R2+r2) | |
| C. | 当磁感应强度大小增大时小圆中感应电流的方向为逆时针 | |
| D. | 当磁感应强度大小增大时小圆中感应电流的方向为顺时针 |
15.据报导,欧洲大型强子对撞机(LHC)定于2008年9月10日开启,并加速第一批质子,该对撞机“开足马力”后能把数以百万计的粒子加速至每秒钟30万公里,相当于光速的99.9%,粒子流每秒可在隧道内狂飙11245圈,单束粒子能量可达7万亿电子伏特.下列说法正确的是( )
| A. | 如果继续对粒子进行加速,粒子的速度将能够达到光速 | |
| B. | 如果继续对粒子进行加速,粒子的速度将能够超过光速 | |
| C. | 粒子高速运动时的质量将大于静止时的质量 | |
| D. | 粒子高速运动时的质量将小于静止时的质量 |
19.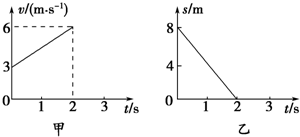 有一个质量为4kg的质点在x-y平面内运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )
有一个质量为4kg的质点在x-y平面内运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )
 有一个质量为4kg的质点在x-y平面内运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )
有一个质量为4kg的质点在x-y平面内运动,在x方向的速度图象和y方向的位移图象分别如图甲、乙所示,下列说法正确的是( )| A. | 质点做匀变速直线运动 | B. | 质点所受的合外力为22 N | ||
| C. | 2 s时质点的速度为6 m/s | D. | 0时刻质点的速度为5 m/s |
9.关于位移和路程,以下说法正确的是( )
| A. | .物体通过一段路程以后,位移必定不为零 | |
| B. | .在直线运动中,位移和路程相同 | |
| C. | .物体的位移为零,说明物体没有运动 | |
| D. | 在质点运动时,位移的大小一定小于或等于路程 |
16.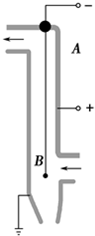 利用静电除尘器可以消除空气中的粉尘.静电除尘器由金属管A和悬在管中的金属丝B组成,A和B分别接到高压电源正极和负极上,其装置示意图如图所示.A、B之间有很强的电场,可以将空气中的粉尘除去.下面关于静电除尘器的说法正确的是( )
利用静电除尘器可以消除空气中的粉尘.静电除尘器由金属管A和悬在管中的金属丝B组成,A和B分别接到高压电源正极和负极上,其装置示意图如图所示.A、B之间有很强的电场,可以将空气中的粉尘除去.下面关于静电除尘器的说法正确的是( )
 利用静电除尘器可以消除空气中的粉尘.静电除尘器由金属管A和悬在管中的金属丝B组成,A和B分别接到高压电源正极和负极上,其装置示意图如图所示.A、B之间有很强的电场,可以将空气中的粉尘除去.下面关于静电除尘器的说法正确的是( )
利用静电除尘器可以消除空气中的粉尘.静电除尘器由金属管A和悬在管中的金属丝B组成,A和B分别接到高压电源正极和负极上,其装置示意图如图所示.A、B之间有很强的电场,可以将空气中的粉尘除去.下面关于静电除尘器的说法正确的是( )| A. | A、B之间的电场是匀强电场 | |
| B. | 距B越近,场强越强 | |
| C. | B附近的气体分子被电离成电子和正离子,粉尘吸附电子后被吸附到A上,最后在重力作用下落入下面的漏斗中 | |
| D. | B附近的气体分子被电离成电子和正离子,粉尘吸附正离子后被吸附到B上,最后在重力作用下落入下面的漏斗中 |
13. 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=2$\sqrt{2}$ m/s | B. | vc=3 m/s | ||
| C. | xde=3 m | D. | 从d到e所用时间为4 s |
14.关于点电荷,下列说法中正确的有( )
| A. | 只要带电的物体,都可以看成点电荷 | |
| B. | 体积很小的带电体就可以看成点电荷 | |
| C. | 体积很大的物体如地球,也可能看成点电荷 | |
| D. | 只要带电体的大小形状可以忽略,就可以看成点电荷 |
