题目内容
【题目】如图,现有一束平行单色光垂直入射到一半径为R的玻璃半球的底面上,O点是半球的球心,虚线OO′是过球心O与半球底面垂直的直线,已知光速为c,玻璃对该色光的折射率为![]() 。
。

①底面上多大区域面积的入射光线能够直接从球面射出?
②某入射光线从距离虚线OO′为0.5R处入射,经球面折射后与OO′有交点,求该光线从进入半球到该交点的运动时间?
【答案】①![]() ②
②![]()
【解析】
(1)根据光路图求解临界角,结合几何关系求解直接从球面射出的入射光线在底面上的面积;(2)根据光路图求解光线传播的距离结合v=c/n求解传播时间.
①如图,从底上面A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角C时,对应光线到光轴的距离最大,设最大距离为d,i=C
设n是玻璃的折射率,由全反射临界角的定义有![]()
由几何关系有![]()
联立解得:![]()
能够直接从球面射出的入射光线在底面上的面积为![]()
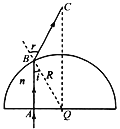
②设与光轴距R/2的光线在球面B点折射时的入射角和折射角分别为i1和r1,
由几何关系有i1=300
由折射定律有sinr1=nsini1
解得:r1=600
即∠BCQ=300可得LBC=R;![]()
且在玻璃半球中![]()
联立得![]()

练习册系列答案
相关题目