题目内容
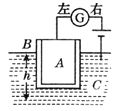
【题目】如图所示，在光滑的水平面上放置一个质量为2m的木板B，B的左端放置一个质量为m的物块A，已知A、B之间的动摩擦因数为μ，现有质量为m的小球以水平速度v0飞来与A物块碰撞后立即粘住，在整个运动过程中物块A始终未滑离木板B，且物块A和小球均可视为质点(重力加速度g)．求：
(1)物块A相对B静止后的速度大小；
(2)板B至少多长．
【答案】(1)0.25v0 (2) 
【解析】小球与A碰撞过程中动量守恒，三者组成的系统动量也守恒，结合动量守恒定律求出物块A相对B静止后的速度大小．
对子弹和A共速后到三种共速的过程，运用能量守恒定律求出木板的至少长度．
设小球和物体A碰撞后二者的速度为v1，三者相对静止后速度为v2，规定向右为正方向，根据动量守恒，得
mv0＝2mv1①
2mv1＝4mv2②
联立①②得，v2＝0.25v0.
当A在木板B上滑动时，系统的动能转化为摩擦热，设木板B的长度为L，假设A刚好滑到B的右端时共速，则由能量守恒，得
·2mv－·4mv＝μ2mgL③
联立①②③式，得L＝
练习册系列答案
相关题目
