题目内容
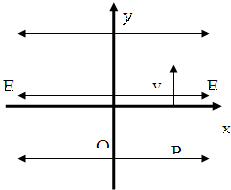 如图所示,在x>0的空间中,存在沿x轴正方向的匀强电场E;在x<0的空间中,存在沿x轴负方向的匀强电场,场强大小也为E.一电子(电荷量大小为e、质量为m.)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:
如图所示,在x>0的空间中,存在沿x轴正方向的匀强电场E;在x<0的空间中,存在沿x轴负方向的匀强电场,场强大小也为E.一电子(电荷量大小为e、质量为m.)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:(1)电子第一次到达y轴时的坐标
(2)电子的x方向分运动的周期.
分析:(1)电子的运动可分解为沿y轴正方向的匀速直线运动和x轴的匀减速运动,由分运动的等时性加以解决
(2)电子沿x方向,先匀加速再匀减速,而后再反向匀加速,再匀减速依次循环往复运动,由对称性可得周期大小
(2)电子沿x方向,先匀加速再匀减速,而后再反向匀加速,再匀减速依次循环往复运动,由对称性可得周期大小
解答:解:(1)电子在x>0的空间中,沿y轴正方向以v0的速度做匀速直线运动,沿x轴负方向做匀加速直线运动,设加速度的大小为a,则:
F=eE=ma
d=
yOA=v0t1
解得:t1=
yOA=v0
即电子第一次到达Y轴时的坐标为解得:yOA=v0
(2)电子从A点进入x<0的空间后,沿y轴正方向仍做v0的匀速直线运动,沿x轴负方向做加速度大小仍为a的匀减速直线运动.根据运动的对称性得,电子x轴方向速度减为零的时间:
t2=t1=
,
所以电子的x方向分运动的周期:
T=4t1=4
答:(1)即电子第一次到达Y轴时的坐标为解得:yOA=v0
(2)电子的x方向分运动的周期为4
F=eE=ma
d=
| 2 1 |
yOA=v0t1
解得:t1=
|
yOA=v0
|
即电子第一次到达Y轴时的坐标为解得:yOA=v0
|
(2)电子从A点进入x<0的空间后,沿y轴正方向仍做v0的匀速直线运动,沿x轴负方向做加速度大小仍为a的匀减速直线运动.根据运动的对称性得,电子x轴方向速度减为零的时间:
t2=t1=
|
所以电子的x方向分运动的周期:
T=4t1=4
|
答:(1)即电子第一次到达Y轴时的坐标为解得:yOA=v0
|
(2)电子的x方向分运动的周期为4
|
点评:本题关键在于把带电粒子的曲线运动应用分解法化曲为直,分析受力情况是解决带电粒子在电场中运动问题的基础

练习册系列答案
相关题目
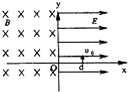 如图所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度正E=10N/C;在x<O的空间中,存在垂直xoy平面方向的匀强磁场,磁感应强度B=0.5T.一带负 电的粒子(比荷q/m=160C/kg),在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,求:
如图所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度正E=10N/C;在x<O的空间中,存在垂直xoy平面方向的匀强磁场,磁感应强度B=0.5T.一带负 电的粒子(比荷q/m=160C/kg),在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,求: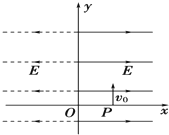 如图所示,在x>0的空间内存在沿x轴正方向的匀强电场,电场强度为E;在x<0的空间内存在沿x轴负方向的匀强电场,场强大小也等于E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:
如图所示,在x>0的空间内存在沿x轴正方向的匀强电场,电场强度为E;在x<0的空间内存在沿x轴负方向的匀强电场,场强大小也等于E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:
