题目内容
一个作自由落体运动的物体,从开始运动起,通过连续的三段路程,所用的时间分别是t、2t、3t,这三段路程的大小之比为:
| A.1:2:3 | B.12:22:32 | C.13:23:33 | D.1:3:5 |
C
分析:求解这三段路程,可以先求第一段的路程,再求前两段的路程,再求前三段的路程;前两段的路程减去第一段的路程,就等于第二段的路程;前三段的路程减去前两段的路程就等于第三段的路程;
物体做匀加速直线运动,可利用推论物体在连续相等的时间内通过的位移之比等于1:3:5:…:(2n-1)加以解答.
解答:解:根据x=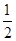 at2可得
at2可得
物体通过的第一段位移为x1=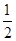 a×1t2
a×1t2
又前2t的位移减去前t的位移就等于第二段的位移
故物体通过的第二段位移为x2=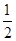 a×(1+2)2t2-
a×(1+2)2t2-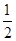 a×1t2=
a×1t2=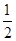 a×8t2
a×8t2
又前6s的位移减去前3s的位移就等于第三段的位移
故物体通过的第三段位移为x3=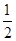 a×(1+2+3)2t2-
a×(1+2+3)2t2-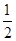 a×(1+2)2t2=
a×(1+2)2t2=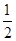 a×27t2
a×27t2
故x1:x2:x3=1:8:27
故选C.
物体做匀加速直线运动,可利用推论物体在连续相等的时间内通过的位移之比等于1:3:5:…:(2n-1)加以解答.
解答:解:根据x=
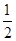 at2可得
at2可得物体通过的第一段位移为x1=
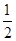 a×1t2
a×1t2又前2t的位移减去前t的位移就等于第二段的位移
故物体通过的第二段位移为x2=
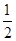 a×(1+2)2t2-
a×(1+2)2t2-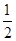 a×1t2=
a×1t2=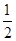 a×8t2
a×8t2又前6s的位移减去前3s的位移就等于第三段的位移
故物体通过的第三段位移为x3=
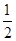 a×(1+2+3)2t2-
a×(1+2+3)2t2-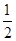 a×(1+2)2t2=
a×(1+2)2t2=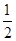 a×27t2
a×27t2故x1:x2:x3=1:8:27
故选C.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 )的速度为5υ
)的速度为5υ υt
υt