Question

10只相同的轮子并排水平排列，圆心分别为O₁、O₂、O₃…O₁₀，已知O₁O₁₀＝3.6m，水平转轴通过圆心，轮子均绕轴以n＝±的转速顺时针转动。现将一根长0.8m、质量为2.0kg的匀质木板平放在这些轮子的左侧，木板左端恰好与O₁竖直对齐（如图所示），木板与轮子间的动摩擦因数为0.16，不计轴与轮间的摩擦，g取10m/s²。求：

（1）木板在轮子上水平移动的总时间；
（2）轮子由于传送木板所多消耗的能量。

Answer 1

（1）2.5s（2）5.12J

解析试题分析：（1）轮子转动的线速度： 
板运动的加速度： 
所以板在轮子上做匀加速运动的时间： 
板在做匀加速运动中所发生的位移： 
板在做匀速运动的全过程中发生的位移为： 
板运动的总时间为： 
（2）由功能关系知：轮子在传送木板的过程中所多消耗的能量一部分转化成了木板的动能，另一部分因克服摩擦力做功转化成了内能，即
木板获得的动能：    
摩擦力做功产生的内能：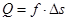   
木板与轮子间的相对位移： 
轮子多消耗的能量：   
联立上述四个方程解得： 
考点：牛顿定律及运动公式的应用；能量守恒定律。