Question

【题目】如图所示，在沿水平方向的匀强电场中有一固定点O，用一根长度为L=0.40m的绝缘细线把质量为m=0.20kg，带有正电荷的金属小球悬挂在O点，电荷量q=0.5C的小球静止在B点时，细线与竖直方向的夹角为θ=37°．（取g=10m/s2，sin37°=0.60，cos37°=0.80）。

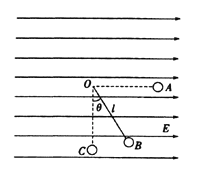
求：（1）匀强电场的场强大小；

（2）将小球拉至位置A使细线水平后由静止释放，小球通过最低点C时细线对小球的拉力大小。

（3）小球静止在B点时，给小球一沿切线方向速度v，求v至少多大才能使球在竖直面内做完整的圆周运动？

Answer 1

【答案】（1）3N/C（2）3N（3）5 m/s

【解析】（1）取小球为研究对象，静止时：

代入数据解得：E=3N/C；

（2）小球从A到C的运动过程由动能定理得：

到达最低点时竖直方向由牛顿第二定律得：

FT﹣mg=m

解得：FT=3N

（3）设恰能到达B关于O的对称点D时，速度最小为vD，则

从B到D,

v= 5 m/s