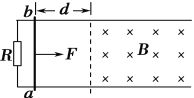��Ŀ����
����Ŀ���ó�ΪL�ľ�Եϸ��˩һ������Ϊm�������Ϊq��С����ͼ��ʾ���ߵ���һ�˹̶���ˮƽ�������ǿ�糡�У���ʼʱ������������ʹ�߳�ˮƽ��λ�ã�С���ɾ�ֹ��A�����°ڶ�����ϸ��ת��60���ǣ�С��B��ʱ���ٶ�ǡ��Ϊ�㣬����
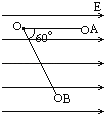
��1����ǿ�糡�ij�ǿEΪ���
��2��С����A�˶���B��Ĺ����У�ϸ�ߵ�����������
��3����A���С��һ��ֱ���µij��ٶ�ʹС���������ֱƽ���ڵ�������Բ���˶�����С���ٶ���С�ĵ�ĵ��ƣ�����O��ĵ���Ϊ�㣬�糡�����㹻��С��ʼ������ǿ�糡�У�
���𰸡���1��![]() ����2����6��2
����2����6��2![]() ��mg����3��
��mg����3��![]()
��������
��1��С���A��B���˶����������ö��ܶ����ģ�
��EqL��1��cos60�㣩+mgLsin60��=0
��ã�E=![]()
��2����С���˶���ϸ�߷�����糡�������������ķ����෴ʱ�����ӵ��������
���ʱ������ˮƽ����н�Ϊ������tan��=![]()
������=30��
���ݶ��ܶ����ã�mgLsin�ȩ�Eq��1��cos�ȣ�L=![]() mv2
mv2
T��F��=m![]()
![]()
��������ʽ��ã�T=��6��2![]() ��mg
��mg
��3��С���ٶ���С�ĵ�Ӧ����Cλ����ͬһֱ���ϵ�C���㣬��ͼ��ʾ
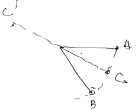
����U=ELsin60��
����=![]()

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ