题目内容
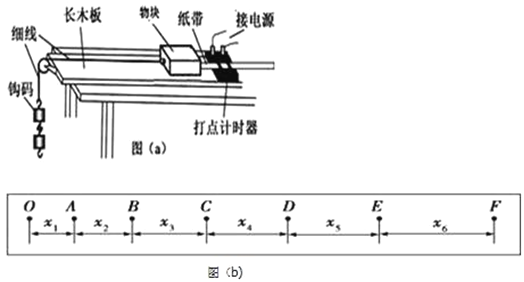
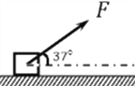
【题目】如图所示,质量M=1kg的木板静置于倾角θ=37°、足够长的固定光滑斜面底端. 质量m=1kg的小物块(可视为质点)以初速度v0=4m/s从木板的下端冲上木板,同时在 木板上端施加一个沿斜面向上的F=3.2N的恒力.若小物块恰好不从木板的上端滑 下,求木板的长度l为多少?已知小物块与木板之间的动摩檫因数μ=0.8,重力加速度 g=10m/s2 , sin37°=0.6,cos37°=0.8.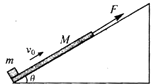
【答案】解:由题意,小物块向上匀减速运动,木板向上匀加速运动,当小物块运动到木板的上端时,恰好和木板共速.
设 小物块的加速度为a,由牛顿第二定律得,mgsinθ+μmgcosθ=ma
设木板的加速度为a′,由牛顿第二定律得,F+μmgcosθ﹣Mgsinθ=Ma′
设二者共速的速度为v,经历的时间为t,由运动学公式得,
v=v0﹣at
v=a′t
小物块的位移为s,木板的位移为s′,由运动学公式得,
s= ![]()
s′= ![]()
小物块恰好不从木板上端滑行,有s﹣s′=l
联立解得l=0.5m.
答:木板的长度l为0.5m
【解析】小物块向上做匀减速运动,木板向上做匀加速直线运动,小物块恰好不从木板的上端滑下,临界情况是到达木板的上端时,速度相同,结合牛顿第二定律,抓住位移关系,结合运动学公式求出木板的长度.
【考点精析】掌握匀变速直线运动的速度、位移、时间的关系和连接体问题是解答本题的根本,需要知道速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值;处理连接题问题----通常是用整体法求加速度,用隔离法求力.