题目内容
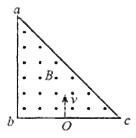
【题目】如图所示，等腰直角三角形abc区域内有垂直纸面向外的匀强磁场，磁感应强度的大小为B，在bc的中点O处有一粒子源，可沿与ba平行的方向发射速率不同的两种粒子，粒子带负电，质量为m，电荷量为q，已知这些粒子都能从ab边离开abc区域，ab=2l，不考虑粒子的重力及粒子间的相互作用，则这些粒子
A. 速度的最大值为
B. 速度的最小值为
C. 在磁场中运动的最短时间为
D. 在磁场中运动的最长时间为
【答案】A
【解析】若都能从ab边出来，则符合条件的最大半径应该与ac面相切，最小半径应该恰好运动到b点，如图所示
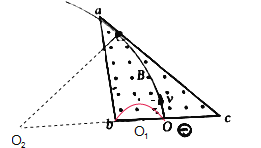
由几何关系可得：
，
AB、粒子在磁场中做圆周运动，洛伦兹力提供了向心力，由牛顿第二定律可得：
解得：
，
，故A对，B错；
C、粒子做圆周运动的周期为
，若圆心角
，则在磁场中的运动时间为
从上图可以看出，最小的圆心角
，所以
，故C错误；
D、 由几何关系知，粒子转过的最大圆心角
，粒子做圆周运动的周期为 所以粒子在磁场中运动的最长时间为
;故D错误；
故选A
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】质量为2kg的物体静止在水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等。t=0时,物体受到方向不变的水平拉力F的作用,F的大小在不同时间段内有不同的值,具体情况如表格所示(g取10m/s2)。求：
时间t/s | 0～2 | 2～4 | 4～6 | 6～8 |
拉力F/N | 4 | 8 | 4 | 8 |
(1)4s末拉力的瞬时功率。
(2)6～8s内拉力所做的功。
(3)8s内拉力的平均功率。