题目内容
【题目】如图所示,在竖直平面内建立xoy坐标系,在第Ⅰ象限内分布着方向沿x轴正方向、大小为E1的匀强电场;在第Ⅱ象限内分布着方向沿y轴正方向、大小E2=![]() 的匀强电场。用长度为L的最大承受拉力为4mg的绝缘细线将质量为m、电荷量为+q的带电小球(可视为质点)悬挂在固定点M,M点坐标为(0,2L),在M点正下方距M点
的匀强电场。用长度为L的最大承受拉力为4mg的绝缘细线将质量为m、电荷量为+q的带电小球(可视为质点)悬挂在固定点M,M点坐标为(0,2L),在M点正下方距M点![]() 的N点处有一钉子。现在用外力把小球拉到右侧与M点等高处由静止释放,小球运动到最低点,绳碰击钉子时刚好被拉断,然后进入第Ⅱ象限,经时间
的N点处有一钉子。现在用外力把小球拉到右侧与M点等高处由静止释放,小球运动到最低点,绳碰击钉子时刚好被拉断,然后进入第Ⅱ象限,经时间![]() ,立即在第Ⅱ象限内再加垂直于xoy平面向里的匀强磁场,磁感应强度为
,立即在第Ⅱ象限内再加垂直于xoy平面向里的匀强磁场,磁感应强度为![]() ,再经过时间t0撤去匀强磁场和匀强电场。(已知重力加速度为g,不计空气阻力,计算结果用g、L、m、q表示)。求:
,再经过时间t0撤去匀强磁场和匀强电场。(已知重力加速度为g,不计空气阻力,计算结果用g、L、m、q表示)。求:
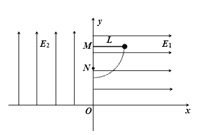
(1)电场强度E1的大小;
(2)小球在下摆过程中达到最大速度时细线的拉力;
(3)小球在第Ⅱ象限中运动的时间t及小球离开第Ⅱ象限的位置坐标。
【答案】(1)![]() (2)
(2)![]() (3)(
(3)(![]() ,0)
,0)
【解析】(1)设小球运动到M点正下方时的速度为v,由动能定理得:
![]()
小球运动到最低点,细线被钉子挡住,做圆周运动的半径为R1,则
由牛顿第二定律有: ![]()
![]()
解得: ![]()
(2)小球在向下摆动的过程中,设合力与竖直方向的夹角为![]() ,当合力方向与速度方向垂直时,即细线与竖直方向的夹角为
,当合力方向与速度方向垂直时,即细线与竖直方向的夹角为![]() 时,速度最大,设为
时,速度最大,设为![]() ,则
,则
![]()
合力![]() ,即
,即![]()
又由动能定理有: ![]()
由牛顿第二定律有: ![]()
解得: ![]()
(3)细线被拉断,小球进入第Ⅱ象限,由于![]() ,所以小球沿水平方向做匀速直线运动。经过时间t0,加上匀强磁场后,小球做匀速圆周运动,设半径为R2,周期为T,则
,所以小球沿水平方向做匀速直线运动。经过时间t0,加上匀强磁场后,小球做匀速圆周运动,设半径为R2,周期为T,则![]() 即:
即: ![]()
![]() 即:
即: ![]()
所以有: ![]()
即小球做圆周运动时间是半个周期,撤去电场和磁场后,小球将做平抛运动穿过x轴。则撤去电场和磁场时,小球的位置坐标为:
![]()
![]()
小球做平抛运动有: ![]()
![]()
故小球离开第Ⅱ象限的位置坐标为(![]() ,0)
,0)
小球在第Ⅱ象限中运动的时间 ![]()
解得: ![]() ,
,
坐标:(![]() ,0)
,0)