题目内容
17.一种氢气燃料的汽车,质量为m=2.0×103kg,发动机的额定输出功率为80kW,行驶在平直公路上时所受阻力恒为车重的0.1倍.若汽车从静止开始先匀加速启动,加速度的大小为=1.0m/s2.达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶.试求:(1)汽车的最大行驶速度;
(2)当速度为5m/s时,汽车牵引力的瞬时功率;
(3)当汽车的速度为32m/s时的加速度.
分析 (1)当牵引力等于阻力时,汽车的速度最大,由功率公式可求得最大行驶速度;
(2)由牛顿第二定律可求得匀速运动时的牵引力,匀加速启动阶段结束时功率达额定功率,由功率公式可求得匀加速结束时的速度,判断速度为5m/s时仍为匀加速过程,则由功率公式可求得牵引力的瞬时功率;
(3)由功率公式可求得速度为32m/s时的牵引力,由牛顿第二定律可求得汽车的加速度.
解答 解:(1)汽车的最大行驶速度vm=$\frac{{P}_{m}}{f}=\frac{80000}{0.1×2000×10}$=40m/s
(2)设汽车匀加速启动阶段结束时的速度为v1,
由F-f=ma,得F=4×103N
由Pm=Fv1,得v1=$\frac{80000}{4000}$=20m/s
匀加速启动的最后速度为20m/s.
所以当速度为5m/s时,处于匀加速阶段,
牵引力的瞬时功率为:P=Fv=20kW
(3)当速度为32m/s时,处于恒定功率启动阶段,设牵引力为F′,加速度为a′
由F′=$\frac{{P}_{m}}{v}=\frac{80000}{32}$=2.5×103N
由F′-f=ma,得a′=0.25m/s2
答:(1)汽车的最大行驶速度为40m/s;
(2)当速度为5m/s时,汽车牵引力的瞬时功率为20kW;
(3)当汽车的速度为32m/s时的加速度为0.25m/s2.
点评 本题考查了汽车启动的匀加速启动方式,注意汽车应经过匀加速、变加速后最后再达到最大速度;并注意动能定理及牛顿第二定律在启动中的应用.

练习册系列答案
相关题目
8.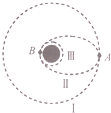 假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )
假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )
 假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )
假设月球半径为R,月球表面的重力加速度为g0.飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点,点火变轨进入椭圆轨道Ⅱ,到达轨道Ⅱ的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.下列判断正确的是( )| A. | 飞船在Ⅱ轨道上由A点运动到B点的过程中,动能增大 | |
| B. | 飞船在轨道Ⅰ上经过A点比在轨道Ⅱ上经过A点加速度小 | |
| C. | 飞船在轨道Ⅲ上经过B点比在轨道Ⅱ上经过B点速度小 | |
| D. | 飞船在轨道Ⅰ绕月球运动一周所需的时间为2π$\sqrt{\frac{64R}{{g}_{0}}}$ |
5.下列物理量不是用比值定义法定义的是( )
| A. | 电场强度E:E=$\frac{F}{q}$ | B. | 电流I:I=$\frac{Q}{t}$ | C. | 电动势E:E=$\frac{W}{q}$ | D. | 加速度a:a=$\frac{F}{m}$ |
2.在如图甲所示的电路中,L1、L2、L3 为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示,当开关 S闭合后,电路中的总电流为0.25A,则( )
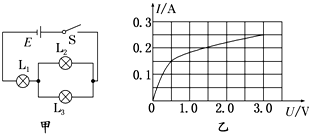

| A. | L1上的电压为L2上电压的2倍 | B. | L1消耗的电功率为0.75 W | ||
| C. | L2的电阻为12Ω | D. | L1、L2消耗的电功率的比值小于4:1 |
6.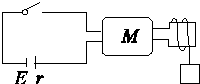 利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )
利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )
 利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )
利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )| A. | 路端电压U大于IR | |
| B. | 电动机提升重物做功的功率为P=UI-I2R | |
| C. | 电源的总功率为P总=$\frac{{E}^{2}}{R+r}$ | |
| D. | 电源的效率为η=$\frac{R}{R+r}$×100% |
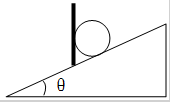 如图所示,质量为16kg的铅球放在光滑的斜面上,用竖直挡板挡住.已知斜面倾角θ=37°,取g=10N/kg,求挡板和斜面对铅球的支持力.(sin37°=0.6,cos37°=0.8)
如图所示,质量为16kg的铅球放在光滑的斜面上,用竖直挡板挡住.已知斜面倾角θ=37°,取g=10N/kg,求挡板和斜面对铅球的支持力.(sin37°=0.6,cos37°=0.8)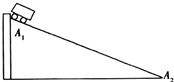 现要验证“当合外力一定时,物体运动的加速度与其质量成反比”这一物理规律.给定的器材如下所示:一倾角可以调节的长斜面(如图所示)、小车、计时器、米尺、弹簧秤,还有钩码若干.实验步骤如下(不考虑摩擦力的影响、重力加速度为g),完成下列实验步骤中所缺的内容:
现要验证“当合外力一定时,物体运动的加速度与其质量成反比”这一物理规律.给定的器材如下所示:一倾角可以调节的长斜面(如图所示)、小车、计时器、米尺、弹簧秤,还有钩码若干.实验步骤如下(不考虑摩擦力的影响、重力加速度为g),完成下列实验步骤中所缺的内容: