题目内容
.如图所示,在水平面上B点的右侧为粗糙的,动摩擦因素为μ,左侧为光滑的。有一质量为m2的小球乙静止放在B点。另一个质量为m1的小球甲以速度v0从A向右运动,与乙球发生对心弹性碰撞后返回。碰撞时间很短,重力加速度为g.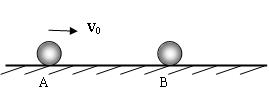
求:(1)碰撞后甲、乙两球的速率。
(2)乙球在平面上刚停下时与甲球间的距离。
(1)v1=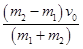 ,v2=
,v2=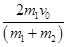 ,(2)S=
,(2)S=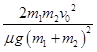
解析试题分析:(1):因为甲、乙两球在B处发生弹性碰撞,故以甲、乙两球为系统的动量守恒,动能不损失,设碰后两球速率分别为V1、V2,取向右方向为正方向,则有:
m1v0= -m1v1+m2v2 ①(2分) ②(2分)
②(2分)
联立①②得v1=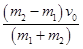 ; (1分)
; (1分)
v2=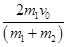 (1分)
(1分)
(2)碰撞后甲球向左做匀速直线运动,设乙球从碰后到停止时的运动时间为t,根据动量定理: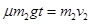 ③(1分)
③(1分)
此时甲、乙两球的距离 ④(1分)
④(1分)
联立③④得S=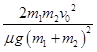 (2分)
(2分)
考点:本题考查了动量守恒和能量守恒的综合应用

 习题精选系列答案
习题精选系列答案下面关于冲量的说法中正确的是( )
| A.物体受到很大的冲力时,其冲量一定很大 |
| B.当力与位移垂直时,该力的冲量为零 |
| C.不管物体做什么运动,在相同时间内重力的冲量相同 |
| D.只要力的大小恒定,其相同时间内的冲量就恒定 |
质量是1 kg的钢球,以5 m/s的速度水平向右运动,碰到墙壁后以3 m/s的速度被反向弹回。假设球与墙面接触的时间是0.1秒,设水平向右为正方向,则( )
| A.钢球的动量变化量为2kg?m/s |
| B.钢球的动量变化量为-2kg?m/s |
| C.墙面对钢球的冲量为8 kg?m/s |
| D.墙面对钢球的冲量为-8 kg?m/s |
下列说法中正确的是( )
| A.合外力的冲量是物体动量变化的原因 |
| B.若合外力对物体不做功,则物体的动量一定不变 |
| C.作用在物体上的合外力越小,物体的动量变化越小 |
| D.发生相互作用的物体,如果不受合外力作用,则每个物体的动量保持不变 |
在光滑的水平桌面上有等大的质量分别为M="0.6" kg,m="0.2" kg的两个小球,中间夹着一个被压缩的具有Ep="10.8" J弹性势能的轻弹簧(弹簧与两球不相连),原来处于静止状态.现突然释放弹簧,球m脱离弹簧后滑向与水平面相切、半径为R="0.425" m的竖直放置的光滑半圆形轨道,如图所示.g取10 m/s2.则下列说法正确的是:
| A.球m从轨道底端A运动到顶端B的过程中所受合外力冲量大小为3.4 N·s |
| B.M离开轻弹簧时获得的速度为9m/s |
| C.若半圆轨道半径可调,则球m从B点飞出后落在水平桌面上的水平距离随轨道半径的增大而减小 |
| D.弹簧弹开过程,弹力对m的冲量大小为1.8 N·s |
质量相等的甲乙两球在光滑水平面上沿同一直线运动。甲以7 kg·m/s的动量追上前方以5 kg·m/s的动量同向运动的乙球发生正碰,则碰后甲乙两球动量不可能的是
| A.6.5 kg·m/s, 5.5 kg·m/s | B.6 kg·m/s, 6 kg·m/s |
| C.4 kg·m/s, 8 kg·m/s | D.5.5 kg·m/s, 6.5 kg·m/s |
一颗手榴弹以v0=10m/s的水平速度在空中飞行。设它爆炸后炸裂为两块,小块质量为0.2 kg,沿原方向以250 m/s的速度飞去,那么,质量为0.4 kg的大块在爆炸后速度大小和方向是
| A.125 m/s,与v0反向 |
| B.110 m/s,与v0反向 |
| C.240 m/s,与v0反向 |
| D.以上答案均不正确 |

