题目内容
6. 如图所示,垂直纸面的两平行金属板M、N之间加有电压,M板上O1处有一粒子源,可不断产生初速度为零的带正电粒子,粒子电荷量为q,质量为m,N板右侧是一半径为R的接地金属圆筒,圆筒垂直于纸面且可绕中心轴逆时针转动.O2为N板上正对O1的小孔,O3、O4为圆筒某一直径两端的小孔,开始时O1、O2、O3、O4在同一水平线上.在圆简上方垂直纸面放置一荧光屏,荧光屏与直线O1O2平行,圆筒转轴到荧光屏的距离OP=3R.不计粒子重力及粒子间相互作用.
如图所示,垂直纸面的两平行金属板M、N之间加有电压,M板上O1处有一粒子源,可不断产生初速度为零的带正电粒子,粒子电荷量为q,质量为m,N板右侧是一半径为R的接地金属圆筒,圆筒垂直于纸面且可绕中心轴逆时针转动.O2为N板上正对O1的小孔,O3、O4为圆筒某一直径两端的小孔,开始时O1、O2、O3、O4在同一水平线上.在圆简上方垂直纸面放置一荧光屏,荧光屏与直线O1O2平行,圆筒转轴到荧光屏的距离OP=3R.不计粒子重力及粒子间相互作用.(1)若圆筒静止且圆筒内不加磁场,粒子通过圆筒的时间为t,求金属板MN上所加电压U;
(2)若圆筒内加垂直纸面向里的匀强磁场,磁感应强度大小为B,圆筒绕中心轴以某一角速度逆时针方向匀速转动,调节MN间的电压使粒子持续不断地以不同速度从小孔O2射出电场,经足够长的时间,有的粒子打到圆筒上被吸收,有的通过圆筒打到荧光屏上产生亮斑.如果在荧光屏PQ范围内的任意位置均会出现亮斑,PQ=$\sqrt{3}$R.求粒子到达荧光屏时的速度大小v的范围;
(3)在第(2)问情境中,若要使进入圆筒的粒子均能从圆筒射出来,求圆筒转动的角速度ω.
分析 (1)对直线加速过程运用动能定理列式;对穿过圆筒过程根据速度公式列式;最后联立求解.
(2)荧光屏PQ范围内的任意位置均会出现亮斑,说明PQ范围内均有粒子到达,最小速度v1的粒子到达P点,最大速度v2的粒子达到Q点;画出轨迹,根据几何关系求解半径,然后根据牛顿第二定律列式求解两个临界速度;
(3)先画出磁偏转的轨迹,求解磁偏转过程的时间,在结合等时性求解圆筒的角速度,得到一般表达式后讨论即可.
解答 解:(1)粒子经电场加速,由动能定理得:
qU=$\frac{1}{2}$mv2 ①
进入圆筒中的粒子有:
t=$\frac{2R}{v}$ ②
由①②得:
U=$\frac{2m{R}^{2}}{q{t}^{2}}$ ③
(2)荧光屏PQ范围内的任意位置均会出现亮斑,说明PQ范围内均有粒子到达,最小速度v1的粒子到达P点,最大速度v2的粒子达到Q点,从PQ间射出的粒子的速度应该含有v1到v2范围内的任意值.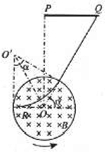
在圆筒中,由牛顿第二定律,有:
qvB=m$\frac{{v}^{2}}{r}$ ④
打到荧光屏上P点的粒子速度:
r1=R ⑤
由④⑤得,到达P点的粒子速度:
v1=$\frac{qBR}{m}$ ⑥
如图由几何关系知到达Q点的粒子穿过圆筒的偏角:
α=60° ⑦
到达Q点的粒子应该满足:
r2=Rtan60° ⑧
到达Q点的粒子速度:
v2=$\frac{qB{r}_{2}}{m}$ ⑨
到达荧光屏的粒子速度大小v的范围:$\frac{qBR}{m}$≤v≤$\frac{\sqrt{3}qBR}{m}$
(3)设粒子穿过圆筒的偏转角为β,则粒子穿过圆筒的时间:
△t=$\frac{β}{2π}$T
又T=$\frac{2πm}{qB}$
粒子穿出圆筒应满足:
ω•△t=β+kπ (k取0,1,2,3…)
ω=(1+$\frac{kπ}{β}$)$\frac{qB}{m}$(k取0,1,2,3…)
粒子速度不同,β不同,要使不同速度的粒子穿过以某一角速度匀速转动的圆筒应该满足:
k=0
即ω=$\frac{qB}{m}$
答:(1)金属板MN上所加电压U为$\frac{2m{R}^{2}}{q{t}^{2}}$;
(2)粒子到达荧光屏时的速度大小v的范围为:$\frac{qBR}{m}$≤v≤$\frac{\sqrt{3}qBR}{m}$;
(3)在第(2)问情境中,若要使进入圆筒的粒子均能从圆筒射出来,圆筒转动的角速度ω为$\frac{qB}{m}$.
点评 本题关键是明确粒子的运动规律,画出临界轨迹,根据牛顿第二定律并结合几何关系列式分析,不难.


| A. | 它们在电场中运动时间相同 | |
| B. | A、B在电场中时间相同,C先飞离电场 | |
| C. | C进入电场的速度最大,A最小 | |
| D. | 电场力对C做功最大 |
 如图,游乐场中,从高处A到水面B处有两条长度相等的光滑轨道,甲、乙两小孩沿着不同轨道同时从A处自由滑向B处,下列说法正确的有( )
如图,游乐场中,从高处A到水面B处有两条长度相等的光滑轨道,甲、乙两小孩沿着不同轨道同时从A处自由滑向B处,下列说法正确的有( )| A. | 甲的切向加速度始终比乙大 | |
| B. | 甲、乙在同一高度的速度大小相等 | |
| C. | 在未到达B处之前的任意时刻甲的速度总是大于乙的速度 | |
| D. | 甲比乙先到达B处 |
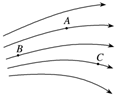
| A. | 最大的是点A,最小的是点B | B. | 最大的是点B,最小的是点C | ||
| C. | 最大的是点C,最小的是点A | D. | A、B、C三点的电场强度方向相同 |
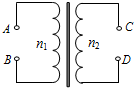 一理想变压器的原线圈A、B两端接入电压为u=3$\sqrt{2}$sin314t V的交变电流.原线圈匝数n1=100匝,副线圈匝数n2=200匝,则( )
一理想变压器的原线圈A、B两端接入电压为u=3$\sqrt{2}$sin314t V的交变电流.原线圈匝数n1=100匝,副线圈匝数n2=200匝,则( )| A. | 将击穿电压为6V的电容器接在C、D两端,不能正常工作 | |
| B. | 把电磁打点计时器接在C、D两端,打点周期为0.01s | |
| C. | 把额定电压为6V的小灯泡接在C、D两端,小灯泡能正常工作 | |
| D. | 把交流电压表接在C、D两端时,电压表读数为8.48V |
 如图所示的是用频闪相机拍下的照片,图中甲、乙两辆汽车都从A处到B处,根据图中提供的信息,汽车从A到B的过程中.甲运动的快慢可用乙的运动来粗略地描述,物理学上把这种科学方法叫做( )
如图所示的是用频闪相机拍下的照片,图中甲、乙两辆汽车都从A处到B处,根据图中提供的信息,汽车从A到B的过程中.甲运动的快慢可用乙的运动来粗略地描述,物理学上把这种科学方法叫做( )| A. | 建立模型法 | B. | 等效替代法 | C. | 无限逼近法 | D. | 微小量放大法 |
 用打点计时器研究匀变速直线运动规律的实验中,得到一条纸带,如图所示,O点为起点,以后每隔5个点取作一计数点.则计数点间的时间间隔为0.1s;若测得OA=2.40Cm,OB=4.2Cm,OC=6.40Cm,则:VC=0.24 m/s,a=0.4 m/s2.
用打点计时器研究匀变速直线运动规律的实验中,得到一条纸带,如图所示,O点为起点,以后每隔5个点取作一计数点.则计数点间的时间间隔为0.1s;若测得OA=2.40Cm,OB=4.2Cm,OC=6.40Cm,则:VC=0.24 m/s,a=0.4 m/s2.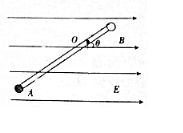 如图所示,在电场强度大小为E,水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动,杆的两端分别固定两电荷量分别为2$\sqrt{3}$q和$\sqrt{3}$q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为3l、l,所受重力大小均为均为其所受电场力大小的$\sqrt{3}$倍,开始时杆与电场方向间夹角θ=30°,将杆从初始位置由静止释放,取O点所在的水平面为重力势能的参考平面,且O点的电势能0,重力加速度为g,求:(结果可保留根号)
如图所示,在电场强度大小为E,水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动,杆的两端分别固定两电荷量分别为2$\sqrt{3}$q和$\sqrt{3}$q的小球A、B,A带正电,B带负电;A、B两球到转轴O的距离分别为3l、l,所受重力大小均为均为其所受电场力大小的$\sqrt{3}$倍,开始时杆与电场方向间夹角θ=30°,将杆从初始位置由静止释放,取O点所在的水平面为重力势能的参考平面,且O点的电势能0,重力加速度为g,求:(结果可保留根号) 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.