题目内容
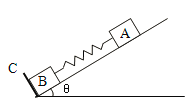
【题目】如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为 mA、mB,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态,现开始用一恒力F沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A受到的合外力和从开始到此时物块A的位移d.(重力加速度为g)
【答案】F﹣(mA+mB)gsinθ, ![]()
【解析】试题分析:物块B刚要离开C时弹簧的拉力等于B的重力沿斜面向下的分力.从而求得物块A受到的合外力.要求从开始到此时物块A的位移d,需要知道弹簧的形变情况,先根据平衡条件和胡克定律求出开始时弹簧的压缩量,再求出物块B刚要离开C时弹簧的伸长量,由几何关系即可求得d.
当物块B刚要离开C时,固定挡板对B的支持力为0,以B为研究对象,由平衡条件有: ![]() ,
,
故此时弹簧弹力大小为![]() .
.
A的受力情况如图,则A所受的合外力 ![]()
在恒力F沿斜面方向拉物块A之前,弹簧的弹力大小为![]() ,
,
故此时弹簧的压缩量为![]()
B刚要离开C时,弹簧伸长量![]() ,
,
所以A的位移![]() .
.

练习册系列答案
相关题目