Question

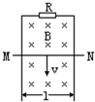如图所示，MN为金属杆，在竖直平面内贴着光滑金属导轨下滑，导轨的间距l=10cm，导轨上端接有电阻R=0.5Ω，导轨与金属杆电阻不计，整个装置处于B=0.5T的水平匀强磁场中．若杆稳定下落时，每秒钟有0.02J的重力势能转化为电能，则MN杆的下落速度v=

 

m/s．

Answer 1

分析：当杆MN达到稳定状态时匀速下滑，重力势能转化为电能，根据能量守恒可知，整个电路消耗的电功率等于MN棒的重力功率，列式即可求得MN杆的下落速度v．

解答：解：杆稳定下落时做匀速运动，重力的功率等于电路的电功率，设重力的功率为P，
由题意有：P=0.02W…①
根据功能关系有：
 P=

E2

R

…②
由法拉第电磁感应定律得：E=Blv… ③
联立①、②、③得：P=

(Blv)2

R

代入数据得：v=2m/s
故答案为：2．

点评：对于电磁感应问题研究思路常常有两条：一条从力的角度，重点是分析安培力；另一条是能量，分析能量如何转化是关键．本题要抓住杆MN达到稳定状态时速率v匀速下滑时，电功率等于重力的功率．