题目内容
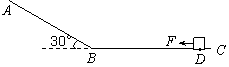
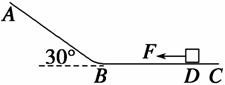
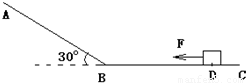
光滑斜面AB与一粗糙水平面BC连接，斜面倾角θ=30°，质量m=2kg的物体置于水平面上的D点，DB间的距离d=7m，物体与水平面间的动摩擦因数μ=0.2，将一水平向左的恒力F=8N作用在该物体上，t=2s后撤去该力，不考虑物体经过B点点时的速度损失．求撤去拉力F后，经过多长时间物体经过B点？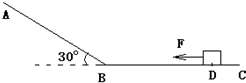
物体在水平面上运动过程：设撤去F前后物体的加速度大小分别为a1、a2，
由牛顿第二定律得：F-μmg=ma1，μmg=ma2，
代入解得a1=2m/s2，a2=2m/s2．
恒力F作用t=2s后物体的位移为x1=
a1t2=4m，
此时物体的速度为v=a1t1=4m/s
设撤去拉力F后，物体第一次经过B点的时间为t1，
则由d-x1=vt1-
a2
代入解得 t1=1s（另一解t1=3s，舍去，根据t1=3s，判断出物体到不了B点）
物体在斜面上运动过程：设加速度大小为a3，
则mgsin30°=ma3，a3=5m/s2．
由上可得物体滑到B点时速度大小为v0=v-a2t1=2m/s
则物体物体在斜面上滑行的总时间t2=
=0.8s
所以物体第二次经过B点的时间为t3=t1+t2=1.8s．
答：撤去拉力F后，物体两次经过B点，第一次时间为1s，第二次时间为1.8s．
由牛顿第二定律得：F-μmg=ma1，μmg=ma2，
代入解得a1=2m/s2，a2=2m/s2．
恒力F作用t=2s后物体的位移为x1=
| 1 |
| 2 |
此时物体的速度为v=a1t1=4m/s
设撤去拉力F后，物体第一次经过B点的时间为t1，
则由d-x1=vt1-
| 1 |
| 2 |
| t | 21 |
代入解得 t1=1s（另一解t1=3s，舍去，根据t1=3s，判断出物体到不了B点）
物体在斜面上运动过程：设加速度大小为a3，
则mgsin30°=ma3，a3=5m/s2．
由上可得物体滑到B点时速度大小为v0=v-a2t1=2m/s
则物体物体在斜面上滑行的总时间t2=
| 2v |
| a3 |
所以物体第二次经过B点的时间为t3=t1+t2=1.8s．
答：撤去拉力F后，物体两次经过B点，第一次时间为1s，第二次时间为1.8s．
练习册系列答案
相关题目
（2012?增城市模拟）光滑斜面AB与一粗糙水平面BC连接，斜面倾角θ=30°，质量m=2kg的物体置于水平面上的D点，DB间的距离d=7m，物体与水平面间的动摩擦因数μ=0.2，将一水平向左的恒力F=8N作用在该物体上，t=2s后撤去该力，不考虑物体经过B点点时的速度损失．求撤去拉力F后，经过多长时间物体经过B点？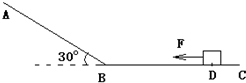
光滑斜面AB与一粗糙水平面BC连接，斜面倾角θ=30°，质量m=2kg的物体置于水平面上的D点，DB间的距离d=7m，物体与水平面间的动摩擦因数μ=0.2，将一水平向左的恒力F=8N作用在该物体上，t=2s后撤去该力，不考虑物体经过B点点时的速度损失．求撤去拉力F后，经过多长时间物体经过B点？
