题目内容
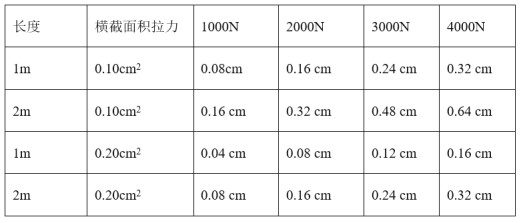
【题目】对一根用新材料制成的金属杆M进行抗拉测量．这根金属杆长5cm，横截面积为1.0cm2，设计要求使它受到拉力后的伸长量不超过原长的
．由于这一拉力很大，杆又很短，直接测试有困难，现选用这种材料制成样品进行测试，得到不同情况下得伸长量如下表所示：
(1)在设计和分析实验数据中，用到了我们学过的_____的科学研究方法．
(2)测试结果表明：样品受拉力作用后，其伸长量与样品的长度成____比，与样品的横截面积成_____比．
(3)待测金属杆M能够允许承受的最大拉力为_____N．
【答案】控制变量法 正 反 125000
【解析】
(1)[1]由题可知伸长量x与样品的长度、横截面积、所受拉力都有关系，涉及的变量较多，因此采用“控制变量法”来确定它们之间的正、反比关系．
(2)[2][3]由表格知：
①、当受到的拉力F、横截面积S一定时，伸长量x与样品长度L成正比，
②、当受到的拉力F、样品长度L一定时，伸长量x与横截面积S成反比，
③、当样品长度L、横截面积S一定时，伸长量x与受到的拉力F成正比，
综上得，样品受拉力作用后，其伸长量与样品的长度成正比，与样品的横截面积成反比．
(3)[4]由上面结论，可以归纳出，x与L、S、F之间存在一定量的比例关系，设这个比值为k，那么有：线材伸长量x与材料的长度L、材料的横截面积S与拉力F的函数关系为
（k为常数）
则：
取S=0.10cm2=1.0×10-5m2，x=0.08cm=8×10-4m，L=1m，F=1000N，则：
k=8.0×10-12m2/N
将金属杆长5cm=0.05m，横截面积为1.0cm2=1×10-4m2，设计要求使它受到拉力后的伸长量不超过原长的
，代入公式得：
F=125000N.
【题目】某同学通过下述实验验证力的平行四边形定则.实验步骤：
①将弹簧秤固定在贴有白纸的竖直木板上，使其轴线沿竖直方向.
②如图1所示，将环形橡皮筋一端挂在弹簧秤的秤钩上，另一端用圆珠笔尖竖直向下拉，直到弹簧秤示数为某一设定值时，将橡皮筋两端的位置标记为O1、O2，记录弹簧秤的示数F，测量并记录O1、O2间的距离(即橡皮筋的长度l).每次将弹簧秤示数改变0.50 N，测出所对应的l，部分数据如下表所示：
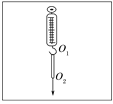
图1
F(N) | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
l(cm) | l0 | 10.97 | 12.02 | 13.00 | 13.98 | 15.05 |
③找出②中F＝2.50 N时橡皮筋两端的位置，重新标记为O、O′，橡皮筋的拉力记为FO O′.
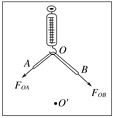
图2
④在秤钩上涂抹少许润滑油，将橡皮筋搭在秤钩上，如图2所示.用两圆珠笔尖成适当角度同时拉橡皮筋的两端，使秤钩的下端达到O点，将两笔尖的位置标记为A、B，橡皮筋OA段的拉力记为FOA，OB段的拉力记为FOB.
完成下列作图和填空：
(1)利用表中数据在图3坐标纸上画出Fl图线________，根据图线求得l0＝________cm.
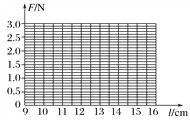
图3
(2)测得OA＝6.00 cm，OB＝7.60 cm，则FOA的大小为________N.
(3)根据给出的标度，在图4中作出FOA和FOB的合力F′的图示_______.
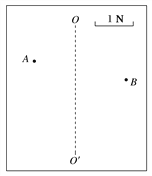
图4
(4)通过比较F′与________的大小和方向，即可得出实验结论.
